Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Коэффициент линейной корреляции и его свойства.

Корреляционная зависимость между случайными величинами Х и Y называется линейной корреляцией, если обе функции регрессии f(x) и φ(x) являются линейными. В этом случае обе линии регрессии являются прямыми; они называется прямыми регрессии.

Для достаточно полного описания особенностей корреляционной зависимости между величинами недостаточно определить форму этой зависимости и в случае линейной зависимости оценить ее силу по величине коэффициента регрессии. Например, ясно, что корреляционная зависимость возраста Y учеников средней школы от года Х их обучения в школе является, как правило, более тесной, чем аналогичная зависимость возраста студентов высшего учебного заведения от года обучения, поскольку среди студентов одного и того же года обучения в вузе обычно наблюдается больший разброс в возраcте, чем у школьников одного и того же класса.

Для оценки тесноты линейных корреляционных зависимостей между величинами Х и Y по результатам выборочных наблюдений вводится понятие выборочного коэффициента линейной корреляции, определяемого формулой:

(7)

где σ_X и σ_Y выборочные средние квадратические отклонения величин Х и Y, которые вычисляются по формулам:

(8)

Следует отметить, что основной смысл выборочного коэффициента линейной корреляции r_B состоит в том, что он представляет собой эмпирическую (т.е. найденную по результатам наблюдений над величинами Х и Y) оценку соответствующего генерального коэффициента линейной корреляции r: r=r_B(9)

Принимая во внимание формулы:

видим, что выборочное уравнение линейной регрессии Y на Х имеет вид:

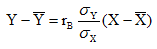(10)

где 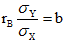. То же можно сказать о выборочном уравнений линейной регрессии Х на Y:

(11)

Основные свойства выборочного коэффициента линейной корреляции:

1. Коэффициент корреляции двух величин, не связанных линейной корреляционной зависимостью, равен нулю.

2. Коэффициент корреляции двух величин, связанных линейной корреляционной зависимостью, равен 1 в случае возрастающей зависимости и -1 в случае убывающей зависимости.

3. Абсолютная величина коэффициента корреляции двух величин, связанных линейной корреляционной зависимостью, удовлетворяет неравенству 0<|r|<1. При этом коэффициент корреляции положителен, если корреляционная зависимость возрастающая, и отрицателен, если корреляционная зависимость убывающая.

4. Чем ближе |r| к 1, тем теснее прямолинейная корреляция между величинами Y, X.

По своему характеру корреляционная связь может быть прямой и обратной, а по силе – сильной, средней, слабой. Кроме того, связь может отсутствовать или быть полной.

Сила и характер связи между параметрами