Читайте также:
|
Относительность движения
Движущиеся тела изменяют своё положение относительно других тел. Положение автомобиля, мчащегося по шоссе, изменяется относительно указателей на километровых столбах, положение корабля, плывущего в море недалеко от берега, меняется относительно береговой линии, а о движении самолёта, летящего над землей, можно судить по изменению его положения относительно поверхности Земли. Механическое движение — это процесс изменения относительного положения тел в пространстве с течением времени. Можно показать, что одно и то же тело может по-разному перемещаться относительно других тел.
Таким образом говорить о том, что какое-то тело движется, можно лишь тогда, когда ясно, относительно какого другого тела — тела отсчета, изменилось его положение.
При́нцип относи́тельности — фундаментальный физический принцип, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.
Отсюда следует, что все законы природы одинаковы во всех инерциальных системах отсчёта.[1]
Различают принцип относительности Эйнштейна (который приведён выше) и принцип относительности Галилея, который утверждает то же самое, но не для всех законов природы, а только для законов классической механики, подразумевая применимость преобразований Галилея, оставляя открытым вопрос о применимости принципа относительности к оптике и электродинамике.
В современной литературе принцип относительности в его применении к инерциальным системам отсчета (чаще всего при отсутствии гравитации или при пренебрежении ею) обычно выступает терминологически как лоренц-ковариантность (или лоренц-инвариантность).
одно и то же движение в различных системах отсчета может выглядеть совершенно по-разному. Для описания движения часто необходимо бывает знать, как при переходе из одной системы в другую меняется мгновенная скорость точки. Правило это и представляет собой содержание так называемой теоремы о сложении скоросте
Рис. 10
Итак, рассмотрим две системы отсчета P и Q, произвольно движущиеся относительно друг друга. Примем условно одну из них, например P, за неподвижную и назовем лабораторной системой, а другую Q, будем считать движущейся. Пусть в подвижной системе точка имеет некую мгновенную скорость, которую назовем относительной скоростью и обозначим как vотн. Чему будет равна ее скорость в лабораторной системе (так называемая абсолютная скорость) vабс, если известно, как движется в данный момент подвижная система относительно неподвижной?
Для ответа на этот вопрос нарисуем два положения 1 и 2 системы Q и точки в ней, разделенные малым интервалом времени t (рис. 10; чтобы не загромождать рисунок, на нем изображено лишь тело отсчета системы Q). Здесь AB= rотн вектор относительного перемещения точки за время t в системе Q. АA перемещение той точки подвижной системы (относительно лабораторной), с которой совпадает в данный момент движущаяся точка; оно называется переносным перемещением и обозначается как rпер. И наконец, АB = rабс абсолютное перемещение точки в системе Р. Из рис. 10, очевидно, rабс= rпер+А B. Разделим теперь это соотношение на t и перейдем к пределу при. При этом по определению скорости
, (15)
где vпер так называемая переносная скорость. Что же касается перемещения А B, то нетрудно видеть, что при безграничном уменьшении t положение 2 системы Q сколь угодно близко подходит к положению 1, а потому вектор А B (уменьшаясь по величине) стремится совпасть с вектором АВ= rотн. Стало быть,
, (16)
и, следовательно,
vабс=vпер+vотн. (17)
Это и есть содержание теоремы о сложении скоростей: абсолютная скорость точки равна векторной сумме ее переносной и относительной скоростей.
Отметим, что приведенный вывод теоремы справедлив в самом общем случае произвольного движения подвижной системы, включая и ее вращение. При этом различные точки Q будут иметь разные скорости. В (17) же входит скорость vпер вполне определенной точки этой системы, а именно той, с которой совпадает в данный момент движущаяся частица.
Пример. С какой минимальной скоростью u должен двигаться автомобиль под дождем, чтобы его заднее стекло оставалось сухим? Скорость капель дождя вертикальна и равна v, стекло наклонено к вертикали под углом (рис. 11).
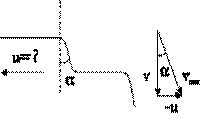рис.11
Найдем скорость капель дождя в движущейся системе координат, связанной с автомобилем. В соответствии с нашими определениями v абсолютная, а u переносная скорости капель. Из (17) их скорость относительно автомобиля
vотн= vабс-vпер= v - u = v +(- u).
Таким образом, в системе, связанной с движущимся автомобилем, дождь окажется уже косым (см. рис.11), причем угол наклона vотн к вертикали тем больше, чем выше скорость автомобиля. Чтобы заднее стекло оставалось сухим, этот угол должен быть, очевидно, не меньше. Отсюда получаем величину минимальной скорости автомобиля u=vtg.
Замечание 1. Напомним еще раз, что мы рассматриваем нерелятивистские, т.е. далекие от световых, скорости. В общем случае произвольных скоростей формулы их преобразования из одной системы в другую заметно усложняются. Из этих формул, в частности, следует, что если vотн=c и vпер=c, где с скорость света, то vабс равна не 2с, как это получалось бы в ньютоновой механике по формуле (17), а тоже с. Движение со скоростями, большими скорости света, невозможно. При vотн, vпер<<c релятивистский закон сложения скоростей, естественно, переходит в (17).
Замечание 2. Наряду с вопросами преобразования скоростей встают аналогичные вопросы с трансформацией ускорений. Будет ли абсолютное ускорение равно сумме относительного и переносного? Да, показывают расчеты, но только при условии, что движущаяся система не вращается.
При наличии вращения формула для ускорений, аналогичная (17), перестает быть справедливой: в ее правой части появляется еще одно слагаемое так называемое кориолисово ускорение, пропорциональное угловой скорости вращения подвижной системы.
3. Кинематика – важный раздел теоретической механики, в котором изучают законы движения материальной точки и абсолютно твердого тела с геометрической точки зрения, без учёта их инерционных характеристик (массы) и действующих на них сил
Кинематику подразделяют на кинематику точки и кинематику абсолютно твердого тела. Если при изучении движения тела его формой и размерами можно пренебречь, то такое тело отождествляют с материальной точкой, т.е. с геометрической точкой, в которой вся масса тела условно считается сосредоточенной. В других случаях тело рассматривают как абсолютно твердое, форму и размеры которого принимают неизменяемыми. Абсолютно твердым телом называют такое тело, расстояние между любыми двумя точками которого при его движении не изменяется.
Дата добавления: 2015-01-30; просмотров: 153 | Поможем написать вашу работу | Нарушение авторских прав |