Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Доказательство.

Пусть удовлетворяют системе (6.28), (6.32), (6.33). Тогда из (6.31) и (6.32) следует, что

и поскольку удовлетворяет (6.33), то

С другой стороны, в силу (6.28) из (6.30) следует, что при любом векторе

Следовательно,

▲

Применяя теорему (6.2), а также положения теории нели­нейного программирования, касающиеся связи между решени­ем экстремальной задачи и существованием седловой точки (см. п. 2.2.2), приходим к выводу о том, что векторы 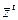, явля­ются решением простейшей задачи оптимального управления (6.27М6.29).

В результате мы получили логически простую схему реше­ния данной задачи: из соотношений (6.32) определяются сопря­женные переменные , затем в ходе решения задачи (6.33) на­ходятся управления и далее из (6.28) — оптимальная траектория состояний .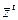

Предложенный метод относится к фундаментальным резуль­татам теории оптимального управления и, как уже это упомина­лось выше, имеет важное значение для решения многих более сложных задач, которые, так или иначе, сводятся к простей­шей. В то же время очевидны и пределы его эффективного ис­пользования, которые целиком зависят от возможности реше­ния задачи (6.33).