
Читайте также:
|
Тема: Основы специальной теории относительности
Ранее мы отмечали роль постулатов в физических теориях и указали, что в число постулатов механики входят законы Ньютона. Однако в число постулатов классической механики входят также и два фундаментальных принципа, касающихся преобразования систем отсчета. Один их них – это принцип относительности Галилея, а другой – принцип инвариантности времени. Рассмотрим эти постулаты.
Принцип относительности Галилея
Эмпирически было надежно установлено, что никакими механическими опытами, проводимыми в инерциальной системе отсчета, невозможно установить, движется эта система или покоится. Это и формулируется в виде принципа относительности Галилея:
Любое механическое явление протекает одинаково во всех инерциальных системах отсчета
Это означает, что не существует особых, выделенных (абсолютных) инерциальных систем отсчета. Все системы отсчета равноправны и относительны. Описание явления, проведенное в любой из них, сохраняет свой принципиальный вид и в любой другой системе отсчета.
| Отобразим на рисунке две инерциальные системы отсчета: К и К '. Для простоты предположим, что эти системы отличаются только движением системы К ' относительно К со скоростью v, направленной только вдоль одной из осей координат (х). Вдоль двух других осей движение не происходит: | 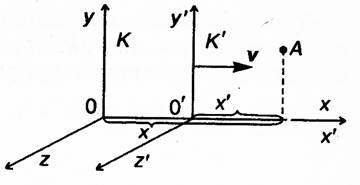
|
Преобразования Галилея. Абсолютное время. Абсолютное пространство
| Если известны координаты и время какого-то события(A)в одной инерциальной системе отсчета К, то можно найти координаты и время этого события в другой инерциальной системе отсчета К '. И наоборот. В классической механике инструментом перехода между системами отсчета служат преобразования Галилея: |  Это прямые преобразования
Это прямые преобразования
 Это обратные преобразования.
Это обратные преобразования.
|
Все физические величины и все уравнения, которые при преобразованиях Галилея остаются неизменными, называются инвариантами преобразований Галилея. Например, инвариантами преобразований Галилея являются ускорения, силы, уравнение 2-го закона Ньютона и др.
К числу таких инвариантов относятся временной интервал между двумя событиями  и пространственный интервал между ними и пространственный интервал между ними  . То есть: . То есть:
| 

|
Эти два выражения равноценны представлениям об абсолютности пространства и времени, которые выработаны и использованы в классической механике:
1) время абсолютно; его ход не зависит от выбора инерциальной системы отсчета, от обстоятельств, связанных с движением систем отсчета;
2) пространство абсолютно; его свойства не зависят от выбора инерциальной системы отсчета, от обстоятельств, связанных с движением систем отсчета.
Дата добавления: 2015-02-16; просмотров: 85 | Поможем написать вашу работу | Нарушение авторских прав |