Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Способы сложения двух сил

Разложение силы на составляющие. Мы уже знаем, как отыскать равнодействующую двух или нескольких заданных сил, направления которых пересекаются.Не менее важна для практики задача о разложении силы на составляющие, т. е. задача отыскания нескольких сил, равнодействующей которых была бы данная сила. Эта задача может приводить к различным решениям, подобно тому как это имеет место при разложении вектора перемещения.

Чтобы задача о разложении силы стала определенной (т. е. имела бы только одно решение), необходимы дополнительные указания. Например, если заданы величина и направление одной из составляющих или два направления, по которым должны действовать составляющие, и т. п., то операция разложения силы на две составляющие становится вполне определенной и сводится к простому геометрическому построению.

Пусть, например, мы хотим разложить силу F на две составляющие, лежащие в одной плоскости с F¹ и направленные вдоль прямых АВ и АС (рис. 104). Для этого достаточно из конца вектора, изображающего F, провести две прямые, параллельные АВ и АС. Отрезки F₁ и F₂ изобразят искомые силы.

Обычно в стоящих перед нами механических задачах содержатся указания на то, как целесообразнее разложить силу на составляющие. Часто условия задачи прямо указывают те направления, по которым нужно найти составляющие данной силы. Например, чтобы отыскать силы натяжения тросов, на которых висит груз, нужно силу тяжести Р груза разложить на составляющие Р₁ и Р₂ по направлениям этих тросов (рис. 105). Натяжения тросов должны уравновесить эти составляющие. Как легко видеть, чем больше угол между тросами, тем больше окажутся силы натяжения тросов. Поэтому если расстояние между опорами тросов велико, то даже небольшой груз, если он висит немного ниже опор, вызывает очень большое натяжение тросов. Этим объясняется, почему гололед или иней иногда обрывает туго натянутые провода.

При разложении силы на три или большее число составляющих увеличивается и число условий, необходимых для того, чтобы разложение было выполнено однозначно.

33)Кинематика точки Кинематика точки – это раздел кинематики, в котором исследуют механическое движение материальной точки. Основная задача кинематики точки состоит в следующем:1) задать закон движения точки, т.е. указать правило, в соответствии с которым можно однозначно определить положение точки в пространстве в любой момент времени по отношению к выбранной системе отсчета;2) по заданному закону движения точки определить все кинематические характеристики ее движения. К характеристикам движения относят траекторию, скорость и ускорение точки. Траектория точки – непрерывная пространственная кривая, которую точка описывает в процессе движения. Если траекторией является прямая линия, то движение называют прямолинейным, если кривая – криволинейным. 1.1. Способы задания движения точки Используют три основных способа задания движения точки: векторный, координатный и естественный. Векторный способ. Положение движущейся точки М в любой момент времени можно определить с помощью ее радиус-вектора, проведенного из центра О, связанного с телом отсчета, в точку М (рис. 1.1). Чтобы задать движение векторным способом, необходимо определить векторную функцию времени в виде:

(1.1)

Зависимость (1.1) называют уравнением движения точки в векторной форме. Начало радиус-вектора движущейся точки находится в точке О, а конец его перемещается по траектории вместе с точкой М. Геометрическое место концов радиус-вектора, т.е. годограф этого вектора, определяет траекторию движущейся точки.

Координатный способ. С телом отсчета связывают прямоугольную систему декартовых координат, при этом положение точки определяют ее координатами, которые являются скалярными функциями времени (рис. 1.2):

(1.2)

Уравнения (1.2) называют уравнениями движения точки в координатной форме. Они являются параметрическими уравнениями траектории точки. Исключив из этих уравнений параметр – время, можно получить уравнение траектории.

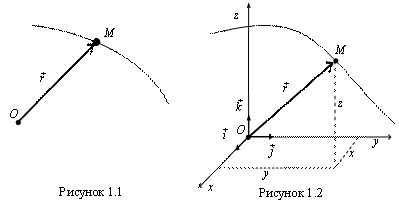
Между способами задания движения точки имеется связь. Так, если начало декартовой системы координат совпадает с центром, из которого проводится радиус-вектор точки при векторном способе изучения ее движения (см. рис. 1.2), то координаты точки равны проекциям на соответствующие оси радиус-вектора точки

,

где – единичные орты координатных осей.

Естественный способ. Этот способ используют в тех случаях, когда заранее известна траектория точки. На траектории выбирают неподвижную точку О (начало отсчета), а также положительное и отрицательное направления отсчета расстояний точки от начала отсчета (рис. 1.3). Тогда положение точки М на траектории будет однозначно определяться зависимостью криволинейной координаты S = ОМ от времени

(1.3)

Связь между координатным и естественным способами определяется выражением

,

где – первые производные от координат точки по времени; С – постоянная интегрирования, зависящая от начальных условий.

34)К простейшим движениям твердого тела относятся поступательное и вращательное. Поступательным называется движение твердого тела, при котором любая прямая, взятая в теле, остается параллельной своему начальному положению. Теорема. При поступательном движении все точки твердого тела описывают одинаковые траектории и имеют в каждый момент времени равные скорости и ускорения. Вращательным называется движение твердого тела, при котором все точки некоторой прямой, связанной с телом, остаются неподвижными во время движения. Эта прямая называется осью вращения. Положение тела определено, если задан угол между плоскостями и , проходящими через ось вращения ( с единичным направляющим вектором ) (рис. 2.2.1). Плоскость неподвижна, а плоскость жестко связана с телом. Угол измеряется в радианах и изменяется с течением времени, – уравнение вращательного движения твердого тела. Угловая скорость характеризует изменение угла поворота с течением времени. Угловое ускорение – характеризует быстроту изменения угловой скорости.

Если угловая скорость постоянна, то вращение называется равномерным и происходит по закону .Если угловое ускорение постоянно, то вращение называется равнопеременным и происходит согласно уравнениям: , .

Модули скорости, ускорения, касательного, нормального ускорений точки вращающегося тела, находящейся на расстоянии от оси вращения, определяются по формулам: , , , , Ускорение точки составляет угол с направлением нормали, при этом

.

35) Основные понятия и аксиомы динамики При изучении динамики используют принципы классической механики, т.е. это механика Ньютона. Пространство: трёхмерное, евклидово. Время абсолютно, пологая, что скорости много меньше скорости света. Сила – количественная мера механического взаимодействия между телами. Масса – физическая величина, зависящая от количества вещества в теле и являющаяся мерой инертности. Масса является скалярной, положительной, постоянной величиной данного тела. Инертность тела – свойство изменять свою скорость, под действием сил, не скачкообразно, а постепенно и тем медленнее, чем больше количество вещества заключено в данном теле. Материальной точкой будем называть математическое тело, размерами которого, в условиях данной задачи, можно пренебречь (для которого различия в скоростях и ускорениях для отдельной его части, при условии данной задачи можно пренебречь). Аксиомы динамики. Первая аксиома динамики (аксиома инерции).

Эту аксиому также называют законом Галилея-Ньютона, так как впервые ее сформулировал Галилей, а Ньютон включил ее в свой трактат как первый закон. Поэтому ее называют и первым законом Ньютона.

Существуют такие системы отсчета, в которых изолированная материальная точка остается в состоянии покоя или равномерного прямолинейного движения.

Эти системы отсчета и являются инерциальными, а связанные с ними системы координат называют инерциальными системами координат. Вторая аксиома динамики (основная аксиома динамики).

Эту аксиому также называют основным законом механики или вторым законом Ньютона.

В инерциальной системе отсчета ускорение материальной точки пропорционально силе, приложенной к ней: ma=F

Коэффициент пропорциональности m между силой и ускорением называется массой материальной точки. Согласно аксиоме инерции, ускорение точки свободной от действия сил равно нулю. Если к точке приложена сила, она выходит из инерциального состояния, приобретая ускорение a = F / m. Поэтому, чем больше масса, тем меньше ускорение и тем больше способность материальной точки сопротивляться действию силы, тем больше ее инерционность. Иначе говоря, масса характеризует инерционность материальной точки и является ее мерой инерции. Третья аксиома динамики (аксиома действия и противодействия). Эту аксиому также называют третьим законом Ньютона. Две материальные точки взаимодействуют друг с другом с силами, равными по величине, направленными по одной прямой в разные стороны. Третья аксиома динамики относится уже к динамике систем материальных точек и тел. Она позволяет глубже проникнуть в сущность понятия силы. В ней сила представляет не только действие, но и противодействие во взаимодействии, как минимум, двух материальных объектов.

Эта аксиома позволяет отличить реальные силы, возникающие при взаимодействии материальных точек, от фиктивных, которые могут появиться при математических преобразованиях в решении задач механики.

Четвертая аксиома динамики (аксиома независимости действия сил).

Эту аксиому часто называют законом независимости действия сил или принципом суперпозиции.

Под действием нескольких сил материальная точка приобретает ускорение, равное геометрической сумме ускорений, которые бы имела точка под действием каждой силы в отдельности.

Согласно аксиоме, несколько сил (F₁, F₂,..., F_n), действующих на материальную точку, можно заменить одной силой F = F₁+ F₂+... + F_n, то есть она аналогична аксиоме параллелограмма сил в статике.