
Читайте также:
|
V. Пусть  – произвольная прямая и
– произвольная прямая и  – точка, не лежащая на ней. Тогда в плоскости, определяемой прямой
– точка, не лежащая на ней. Тогда в плоскости, определяемой прямой  и точкой
и точкой  , существует не более одной прямой, которая проходит через точку
, существует не более одной прямой, которая проходит через точку  и не пересекает прямую
и не пересекает прямую  (аксиома Плейфера).
(аксиома Плейфера).
Следует заметить, что геометрию, построенную на аксиомах групп
1–1V, называют абсолютной геометрией. Эту геометрию составляют все предложения школьного курса геометрии, которые доказываются без помощи аксиомы параллельности.
На основе аксиом всех пяти групп изучаются свойства параллельных прямых по Евклиду, доказываются теоремы о сумме углов треугольника и выпуклого многоугольника, изучаются свойства параллелограммов и трапеций, строится теория подобия и т. д. Также аксиомы групп 1–V позволяют обосновать тригонометрию, изучаемую в средней школе, и координатный метод в геометрии. В частности, теорема Пифагора, для доказательства которой необходимо использовать аксиому V, позволяет вывести формулу для вычисления расстояния между двумя точками по координатам этих точек и решать большое число задач аналитической геометрии.
Первая неевклидова геометрия была построена русским математиком, профессором Казанского университета, Николаем Ивановичем Лобачевским.
Н.И. Лобачевский родился 2 декабря 1792 г. в Нижнем Новгороде. С 1802 по 1807 г. учился в Казанской гимназии, с 1807 по 1811 г. состоял студентом незадолго до того основанного в Казанского университета, с 1814 г. – адъюнкт, с 1816 г. – профессор того же университета, с 1827 по 1846 г.– его ректор. С 1846 по 1855г. – помощник попечителя Казанского учебного округа. Скончался Н.И. Лобачевский 24 февраля 1856 г.
В течение первых лет преподавательской деятельности в Казанском университете Н.И. Лобачевский настойчиво пытался доказать V постулат Евклида: «Если прямая, пересекающая две прямые, образует внутренние односторонние углы, в сумме меньшие двух прямых углов, то эти две прямые пересекаются с той стороны, где сумма углов меньше двух прямых»(Заметим, что это предложение равносильно аксиоме параллельности). Неудача этих попыток привела его к выводу о том, что V постулат Евклида нельзя вывести из остальных аксиом. Лобачевский отвергает этот постулат и заменяет его следующей аксиомой.
V*(аксиома Лобачевского). Пусть даны прямая и точка, не лежащая на ней. Тогда в плоскости, проходящей через прямую и точку,существует не менее двух прямых, проходящих через точку и не пересекающих прямую.
Используя эту аксиому и аксиомы абсолютной геометрии, то есть все остальные аксиомы геометрии, кроме аксиомы параллельности евклидовой геометрии, Лобачевский чисто логически строит новую геометрию, которую называет «воображаемой» (позднее ее стали называть геометрией Лобачевского).
Укажем некоторые факты геометрии Лобачевского. Не надо удивляться, что эти предложения противоречат известным теоремам Евклида. Ведь геометрия Лобачевского отражает свойства поверхности, отличной от евклидовой плоскости. Поверхность, на которой выполняется созданная Лобачевским геометрия, самому ему была неизвестна, она открыта только после его смерти.
Теорема 1. Во всяком треугольнике сумма внутренних углов меньше 2d.
Теорема 2. Во всяком выпуклом четырехугольнике сумма внутренних углов меньше 4d.
Теорема 3. Сумма углов треугольника непостоянна, т. е. не одна и та же для всех треугольников.
Теорема 4. Если три угла одного треугольника соответственно равны (конгруэнтны) трем углам другого треугольника, то эти треугольники равны (4-ый признак равенства треугольников).
Теорема 5. Через каждую точку  , не лежащую на прямой
, не лежащую на прямой  , в плоскости, определяемой этой прямой и точкой, можно провести в точности две прямые, параллельные данной прямой
, в плоскости, определяемой этой прямой и точкой, можно провести в точности две прямые, параллельные данной прямой  .
.
Теорема 6. На плоскости существуют треугольники, около которых нельзя описать окружность.
Теорема 7. Внутри любого острого угла существуют точки, через которые нельзя провести прямую, одновременно пересекающую обе стороны этого угла.
Теорема 8. Расстояние от точек одной из параллельных прямых до другой в одну сторону неограниченно убывает, а в другую сторону неограниченно растет.
Результаты Лобачевского оказались настолько необычными для умов, воспитанных на идеях геометрии Евклида, что не были поняты большинством из его современников.
Примерно в одно время с Н.И. Лобачевским (первая половина 19 века)к открытию неевклидовой геометрии подошли немецкий математик К.Гаусс и венгерский ученый Янош Бойяи.
Задачи
10. Есть ли в реальном мире точки, прямые, плоскости?
11. В чем отличие аксиом от теорем?
12. Почему аксиомы не доказываются?
13. Существуют ли для одной и той же теории разные наборы аксиом?
14. Можно ли вместо одних основных неопределяемых понятий взять другие?
15. В чем отличие в аксиоматических построениях геометрии Евклида и геометрии Лобачевского?
16. Что называется моделью аксиоматической теории?
17. Взяв в качестве точек вершины треугольной пирамиды, сформулируйте несколько возможных аксиом евклидовой геометрии треугольной пирамиды.
18. Постройте какую-нибудь модель следующей системы аксиом.
Даны объекты первого и второго рода и отношение «объект 1 рода принадлежит объекту 2 рода», удовлетворяющие следующим аксиомам:
1) существуют, по крайней мере, 3 объекта 1 рода;
2) каждому объекту 2 рода принадлежат в точности два объекта 1 рода.
19. Задача «Города и маршруты». Некоторая организация продает путевки путешествий по городам. В схему путешествий, по которым составляются маршруты, входят 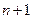 городов. Принципы составления маршрутов таковы:
городов. Принципы составления маршрутов таковы:
1) для любых двух городов существует единственный маршрут, через них проходящий;
2) каждые два маршрута имеют общий город.
Возможно ли и при каких  построение такой схемы путешествий?
построение такой схемы путешествий?
20. Добавьте к принципам составлениясхемы путешествий задачи 15 еще один: 3) не должно быть такого маршрута, который бы проходил через все города, кроме одного.
При таком добавлении: а) составьте схему путешествий для  ; б) докажите, что для схемы путешествий, удовлетворяющей трем сформулированным выше принципам, справедливы следующие утверждения:
; б) докажите, что для схемы путешествий, удовлетворяющей трем сформулированным выше принципам, справедливы следующие утверждения:
1) Если какой-нибудь маршрут содержит  город, то и всякий маршрут содержит
город, то и всякий маршрут содержит  город;
город;
2) каждый город входит в  маршрут;
маршрут;
3) существуют 4 города, никакие 3 из которых не принадлежат одному маршруту.
В предложениях 2 и 3 предполагается, что выполнено утверждение 1.
21. Группа, состоящая из 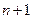 ученика, участвует в дежурствах. График дежурств составлен по следующим правилам:
ученика, участвует в дежурствах. График дежурств составлен по следующим правилам:
1)любые два ученика должны участвовать в единственном общем дежурстве;
2) в любых двух дежурствах есть общий ученик;
3) нет дежурств, в которых принимает участие  учеников.
учеников.
Составьте график дежурств для группы из  учеников.
учеников.
Вывод из задач 19 – 21. Задачи 19–21 представляют собой модели одной абстрактной аксиоматической системы (обозначим ее символом  ).
).
Если основные объекты этой системы назвать точками и прямыми, а основное отношение между ними – отношением инцидентности или принадлежности, то эту систему аксиом составляют следующие предложения:
11. Для любых двух различных точек  и
и  существует единственная прямая
существует единственная прямая  , им инцидентная (принадлежащая каждой из этих двух точек).
, им инцидентная (принадлежащая каждой из этих двух точек).
12. Для любых двух различных прямых существует точка, им инцидентная.
13. Существует, по крайней мере, одна прямая. Несуществует прямой, инцидентной всем точкам за исключением одной.
22. Докажите, что из этой системы аксиом вытекают следующие предложения – теоремы:
1) любые две различные прямые имеют одну и только одну общую точку;
2) существуют такие 4 точки, что всевозможные пары из них определяют 6 различных прямых;
3) существуют 4 различные прямые, из которых никакие 3 не имеют общей точки.
4) всякая прямая имеет, по меньшей мере, 3 точки; всякая точка принадлежит, по меньшей мере, трем прямым.
Дата добавления: 2015-02-16; просмотров: 112 | Поможем написать вашу работу | Нарушение авторских прав |