Теорема Ферма.
Если функция у = f (х), определенная в интервале (а; b), достигает в некоторой точке с этого интервала наибольшего (или наименьшего) значения и существует производная f ′(с), то f ′(с) = 0.
Геометрический смысл этой теоремы состоит в том, что касательная к графику функции у = f (х) в точке с абсциссой с параллельна оси абсцисс (рис.).
Равность нулю производной - необходимое условие существования экстремума, но не достаточное. То есть производная может быть равной 0 и вне точки экстремума. Пример: 
, но точка 0 - не экстремум.
Теорема Ролля.
Если функция у = f (х), непрерывная на отрезке [ а; b ] и дифференцируемая в интервале (а; b), принимает на концах этого отрезка равные значения f (a) = f (b), то в интервале (а; b) существует такая точка с, что f ′(с) = 0.
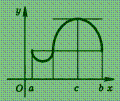
Геометрически эта теорема означает следующее: если крайние ординаты кривой у = f (х) равны, то на кривой найдется точка, в которой касательная параллельна оси абсцисс (рис.).
Теорема Лагранжа. Если функция у = f (х) непрерывна на отрезке [ а; b ] и дифференцируема в интервале (а; b), то в этом интервале найдется такая точка с, что 
Эта теорема имеет простой геометрический смысл (рис.): на графике функции у = f (х) между точками А и В найдется такая внутренняя точка С, что касательная к графику в точке С параллельна хорде AB.
Следствие. Если f ′(x) = 0 в интервале (а; b), то в этом интервале функция f (х) постоянна.
Теорема Коши. Если функции f (х) и g (х): 1) непрерывны на отрезке [ а; b ];
2) дифференцируемы в интервале (а; b);
3) g' (x) ≠ 0 в этом интервале,
то в интервале (а; b) существует такая точка с, что имеет место равенство
Дата добавления: 2015-02-16; просмотров: 82 | Поможем написать вашу работу | Нарушение авторских прав |