Читайте также:
|
ФИЗИЧЕСКИЕ ОСНОВЫ ЭРОЗИИ ПОЧВ
Живое сечение потока w - поперечное сечение потока, перпендикулярное к линиям тока, его пересекающим (в см2 или м2).
Периметр смоченности х - длина линии контакта живого сечения с ложем потока (в м или см). Гидравлический радиус R – отношение площади живого сечения к периметру смоченности (в м).
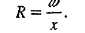
Широкие русла=> х мало отличается от ширины потока(b), =>R≈H(глубина потока)
Для прямоугольного русла: 
Если Ь»Н, то слагаемым 2H можно пренебречь=>
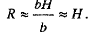
Расход потока Q - объем воды, протекающей через поперечное сечение потока в единицу времени
(в м3/с или л/с).
Скорость потока V - длина пути, проходимого водой в единицу времени (в м/с или см/с).
Связь между расходом,скоростью и живым сечением потока.
Выберем в потоке элемент ABCD живого сечения площадью w. все его Предположим,что все точки перемещаются с одной и той же скоростью и. => за единичный промежуток времени выбранный элемент сечения переместится на расстояние и => займет положение KLMN.
Q=uw -объем воды, прошедшей через сечение ABCD в единицу времени
Реальные условия: скорость в разных точках живого сечения не постоянна. В открытых потоках (имеют пов-ть раздела вода-воздух) max скорость потока вблизи пов-ти, min - у дна=>вводится понятие средней скорости Vср .- фиктивная, постоянная для всех точек живого сечения скорость потока, при которой расход воды такой же, как и при истинном распределении скоростей.
Q = Vw, т.е. расход потока (м3/с) в данном сечении равен произведению площади живого сечения (м2) на среднюю скорость в этом сечении (м/с).
Режимы течения
Ламинарный режим -упорядоченное параллельноструйное движением без образования вихрей. Турбулентный режим- хаотически беспорядочное движение, струи постоянно отклоняются и пересекаются друг с другом. Скорость в турбулентном потоке непрерывно пульсирует,изменяясь как по величине, так и по направлению(но направление поступательного движения всего потока остается неизменным).Скорость потока в данной точке при этом колеблется около некоторого постоянного, не зависимого от времени, значения - усредненной скорости й'.
Мгновенная скорость- скорость в каждый данный момент времени в заданной точке.
Пульсацию продольных составляющих скорости течения можно описать кривой нормального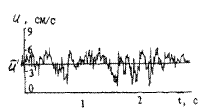 
распределения,при этом выполняется соотношение и'тах - й ' ~ Зσ, где и'тах -максимальная пульсационная скорость, и ' - усредненная скорость, σ – среднеквадратичное отклонение.
Для измерения пульсации скоростей в потоке применяются приборы термоанемометры. Принцип действия: интенсивность теплообмена между потоком и введенным в него телом, а с ним и электрическое сопротивление этого тела, зависит от скорости течения.
У тв. стенки даже в турбулентных потоках есть тонкий слой, в котором скорости и пульсационыне = 0. Выше: тонкий пристеночный слой - вязкий подслой потока, который отличается по своим свойствам от основной толщи потока- турбулентное ядро.
Показатель степени турбулентности - безразмерное число Рейнольдса Re, опред. по формуле:
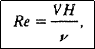где Н - глубина потока, м; V- скорость течения, м/с; ν- кинематическая
вязкость (при t = 20°С для воды ν = 10-6 м2/с).
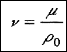где μ - динамическая вязкость жидкости (коэффициент внутреннего трения), ρ0 - ее плотность.
Плотность жидкости и ее вязкость уменьшаются при повышении температуры.
Для потоков с открытой водной пов-тью ламинарный режим при Re <300, турбулентный - при Re >600. При 300 <Re < 600 - либо турбулентный, либо ламинарный (в зависимости от шероховатости и характера русла).
Пульсацию скорости в турбулентных потоках учитывают путем введения соответствующего коэффициента в уравнение критической скорости потока.
В природных условиях: 1) ламинарные потоки - на хорошо задернованных склонах (вода течет ровным слоем малой глубины с небольшими скоростями); на распаханных склонах в начальной фазе снеготаяния (талая вода испытывает на своем пути сопротивление снега); фильтрационные потоки (малый диаметра пор и незначительная скорость). 2) турбулентное движение - в текущих
водах и в атмосфере, с ним и связаны процессы водной и ветровой эрозии.
Закономерности движения жидкости
Значит. роль в ламинарном движении жид-ти принадлежит ее вязкости => формируется непрерывное скоростное поле потока, происходит поглощение части мех. энергии потока и переход ее в тепловую, т.е. диссипация энергии - источник гидродинамического сопротивления.
Основное уравнение теории вязкого потока жидкости, установленное Ньютоном, показывает, что при стационарном движении действующая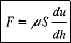 
сила F уравновешивается силами внутреннего трения жидкости(1): где S - величина поверхности сдвига, μ - коэффициент внутреннего трения, и -скорость потока, h - расстояние от дна.
Введя касательное напряжение трения τ = F/S, имеем: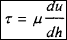 
что ур. справедливо для "ньютоновских" жид-тей (вода, глицерин, масло, нефть)(2). Неньютоновские жид-ти: для суспензий с большимкол-вом тв. частиц движение начинается лишь при достижении некоторой величины касательного напряжения (напряжения сдвига, τ0)(3):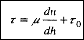 
Равномерное течение жид-ти по очень широкому прямоугольному руслу, наклоненному под углом αк гор-ту. На столб жид-ти, имеющий основанием ед.пов-ти русла, действуют две противоположно направленные силы, параллельные дну.
1. Составляющая силы тяжести, F = Р Sin α. Вес столба воды, приведенньй к единице пов-ти дна Р=ρogH, где ρо - плотность воды, кг/м3; g - ускорение силы тяжести, м/с2; Н – глубина потока, м. =>обозначив Sin α через I => F = ρogHI.
2. Сила внутреннего трения жидкости (τ, Н/м2).Рассматривается равномерное движение жидкости=>эти силы можно приравнять=> PogHI = τ
· При ламинарном движении жид-ти сила внутреннего трения прямо пропорциональна динамической вязкости и отношению средней скорости потока V к его глубине в первой степени.
=> ρogHI = 3μV/H, где v - кинематическая вязкость (м2/с). Зависимость Пуазейля.
· При турбулентном режиме течения жид-ти сопротивление прямо пропорционально ее плотности и средней скорости в квадрате=> ρogHI = AρoV2 где А – безразм. коэфф
Если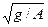 
= С, => формула Шези: 
при Н ~ R => V = C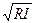 
, где V - средняя скорость потока, м/с; С - коэффициент Шези, м0,5/с; R - гидравлический радиус, м; Н - глубина потока, м; I – Sinα, где α -угол наклона водной пов-ти, который при равномерном движении равен углу наклона склона; при малых значениях Sinα ≈ tgα≈ I.
Оба уравнения (Пуазейля и Шези) описывают равномерное движение потокаглубиной Н при уклоне водной поверхности I, однако их структура резко различается:
1. В первом случае глубина возведена в квадрат, вовтором - в степень 0,5=> в первом случае ее влияние гораздобольше, чем во втором.
2. Уклон в уравнении Пуазейля стоит в более высокой степени, чем в Шези
3. В уравнении Пуазейля скорость движения зависит от вязкости, а в уравнении Шези - не зависит.
В турбулентных потоках кроме молекулярной вязкости появляется турбулентная вязкость (τ т), обусловленная перемешиванием жид-ти, приводящим к возникновению дополнит. сил сопротивления на пов-ти взаимодействия слоев. Полное касательное напряжение трения (τ п), выражается ур: τ п = τ т+τ, т.к. первый член ур >> второго=>τ п≈τ т.
Для расчета коэффициента Шези используют ряд эмпирических формул.
1.Формула Маннинга( простая):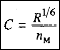 
где n м - коэффициент шероховатости.
2. Формула Павловского( сложная,сокращенная)
Ф-ла Маннинга - частный случай ф-лы Павловского 
при n п = 0,012. Эти формулы применяются для расчета скорости движения воды в каналах, во временной оросительной сети.
Для расчета скорости движения потоков на склонах при дождях и снеготаянии ф-ла Базена: где пБ - коэффициент шероховатости.
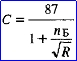
Дата добавления: 2015-04-20; просмотров: 93 | Поможем написать вашу работу | Нарушение авторских прав |