
1. Линейная функция. Это функция вида 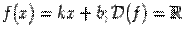 . Число
. Число  называется угловым коэффициентом, а число
называется угловым коэффициентом, а число 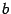 -- свободным членом. Графиком
-- свободным членом. Графиком 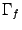 линейной функции служит прямая на координатной плоскости
линейной функции служит прямая на координатной плоскости 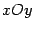 , не параллельная оси
, не параллельная оси 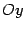 .
.
Угловой коэффициент  равен тангенсу угла
равен тангенсу угла 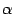 наклона графика
наклона графика 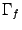 к горизонтальному направлению -- положительному направлению оси
к горизонтальному направлению -- положительному направлению оси 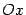 .
.
Рис.1.8.График линейной функции -- прямая
2. Квадратичная функция. Это функция вида 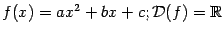 (
(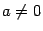 ).
).
Графиком 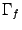 квадратичной функции служит парабола с осью, параллельной оси
квадратичной функции служит парабола с осью, параллельной оси 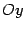 . При
. При 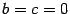 вершина параболы оказывается в точке
вершина параболы оказывается в точке 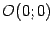 .
.
Рис.1.9.Парабола 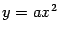 (
(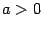 )
)
В общем случае вершина лежит в точке 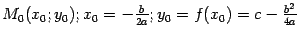 . Если
. Если 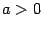 , то "рога" параболы направлены вверх, если
, то "рога" параболы направлены вверх, если 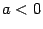 , то вниз.
, то вниз.
Рис.1.10.Парабола с вершиной в точке 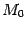 (
(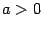 )
)
3. Степенная функция. Это функция вида 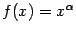 ,
, 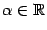 . Рассматриваются такие случаи:
. Рассматриваются такие случаи:
а). Если 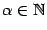 , то
, то 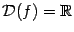 . Тогда
. Тогда 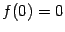 ,
,  ; если число
; если число 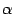 -- чётное, то и функция
-- чётное, то и функция 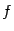 -- чётная (то есть
-- чётная (то есть 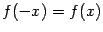 при всех
при всех 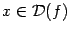 ); если число
); если число 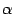 -- нечётное, то и функция
-- нечётное, то и функция 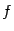 -- нечётная (то есть
-- нечётная (то есть  при всех
при всех 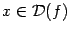 ).
).
Рис.1.11.График степенной функции при 
б). Если  ,
,  , то
, то 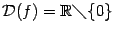 . Ситуация с чётностью и нечётностью при этом такая же, как и для
. Ситуация с чётностью и нечётностью при этом такая же, как и для 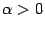 : если
: если 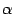 -- чётное число, то и
-- чётное число, то и  -- чётная функция; если
-- чётная функция; если 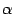 -- нечётное число, то и
-- нечётное число, то и  -- нечётная функция.
-- нечётная функция.
Рис.1.12.График степенной функции при 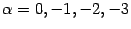
Снова заметим, что  при всех
при всех 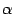 . Если
. Если 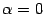 , то
, то 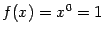 при всех
при всех 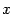 , кроме
, кроме 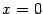 (выражение
(выражение 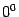 не имеет смысла).
не имеет смысла).
в). Если 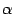 -- не целое число, то, по определению, при
-- не целое число, то, по определению, при 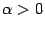 :
: 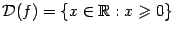 ; тогда
; тогда 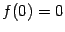 ,
,  .
.
Рис.1.13.График степенной функции при 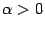
При 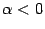 , по определению,
, по определению, 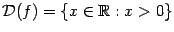 ; тогда
; тогда  .
.
Рис.1.14.График степенной функции при 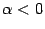
Е.А. Егорова_/ 15.09.2014
подпись расшифровка подписи дата заполнения
Дата добавления: 2014-11-24; просмотров: 92 | Поможем написать вашу работу | Нарушение авторских прав |