При изотермическом процессе, температура рабочей среды постоянна. Изотермический процесс можно выразить через уравнение идеального газа следующим образом
p / ρ = constant (1)
где p = абсолютное давление
ρ = плотность
Или так
pV = constant (1a)
или
p1V1 = p2V2 (1b)
где V = объем газа (м3, фут 3...)
индекс1 относится к начальному состоянию рабочей среды, а индекс 2 к конечному
4. Обратимые и необратимые процессы, пути изменения состояния термодинамической системы. Процесс называют обратимым, если он допускает возвращение рассматриваемой системы из конечного состояния в исходное через ту же последовательность промежуточных состояний, что и в прямом процессе, но проходимую в обратном порядке. При этом в исходное состояние возвращается не только система, но и среда. Обратимый процесс возможен, если и в системе, и в окружающей среде он протекает равновесно. При этом предполагается, что равновесие существует между отдельными частями рассматриваемой системы и на границе с окружающей средой. Обратимый процесс - идеализированный случай, достижимый лишь при бесконечно медленном изменении термодинамических параметров. Скорость установления равновесия должна быть больше, чем скорость рассматриваемого процесса. Если невозможно найти способ вернуть и систему, и тела в окружающей среде в исходное состояние, процесс изменения состояния системы называют необратимым.
Необратимые процессы могут протекать самопроизвольно только в одном направлении; таковы диффузия, теплопроводность, вязкое течение и другое. Для химической реакции применяют понятия термодинамической и кинетической обратимости, которые совпадают только в непосредственной близости к состоянию равновесия. Р-ция А + В С + D наз. кинетически обратимой или двусторонней, если в данных условиях продукты С и D могут реагировать друг с другом с образованием исходных веществ А и В. При этом скорости прямой и обратной реакций, соотв., где и -константы скорости, [А], [В], [С], [D]- текущие концентрации (активности), с течением времени становятся равными и наступает химическое равновесие, в котором -константа равновесия, зависящая от температуры. Кинетически необратимыми (односторонними) являются обычно такие реакции, в ходе которых хотя бы один из продуктов удаляется из зоны реакции (выпадает в осадок, улетучивается или выделяется в виде малодиссоциированного соединения), а также реакции, сопровождающиеся выделением большого кол-ва тепла.
На практике нередко встречаются системы, находящиеся в частичном равновесии, т.е. в равновесии по отношению к определенного рода процессам, тогда как в целом система неравновесна. Например, образец закаленной стали обладает пространственной неоднородностью и является системой, неравновесной по отношению к диффузионным процессам, однако в этом образце могут происходить равновесные циклы механической деформации, поскольку времена релаксации диффузии и деформации в твердых телах отличаются на десятки порядков. Следовательно, процессы с относительно большим временем релаксации являются кинетически заторможенными и могут не приниматься во внимание при термодинамич. анализе более быстрых процессов.
Функции «внутренняя энергия» и «энтальпия» не дают однозначного ответа на вопрос о возможности самопроизвольного протекания процесса.
Из уравнения (1.3.) следует, что при изменении внутренней энергии системы максимальному значению работы будет соответствовать минимальное значение теплоты (по абсолютной величине). Отношение этой минимально возможной теплоты к температуре, при которой осуществляется изотермический процесс, называется приведенной теплотой.
Энтропия представляет собой функцию состояния систем, приращение которой (ΔS) равно теплоте Qмин), подведенной к системе в изотермическом процессе, деленной на абсолютную температуру (Т), при которой осуществляется процесс:
где Qмин - минимальное приращение теплоты, подведенное к системе.
5. Наиболее общая формулировка второго начала термодинамики была дана позже. Она носит название «принцип возрастания энтропии» (или «неравенство Клаузиуса»). Дадим эту формулировку без использования понятия энтропия: любые процессы, происходящие в замкнутой системе, переводят ее из более упорядоченного в более беспорядочное (хаотическое) состояние. Замкнутой системой называется такая система, которая не обменивается с окружающей средой веществом и (или) энергией.
Таким образом, второе начало термодинамики указывает направление происходящих в замкнутых системах процессов: возможны лишь такие процессы, которые приводят к возрастанию хаоса и беспорядка в замкнутых системах, к снижению уровня их организованности. Именно поэтому говорят, что второе начало термодинамики определяет термодинамическую стрелу времени. Для замкнутых систем нормальному ходу времени соответствуют процессы, приводящие к увеличению хаоса и беспорядка в этих системах.
Дадим теперь формулировку второго начала термодинамики, используя понятие «энтропия». Понятие «энтропия» сегодня настолько широко используется в научно-популярной литературе, что можно сказать: это понятие стало частью общей культуры, а не просто научным термином.
Энтропия – это физическая величина, которая характеризует степень неупорядоченности любой системы: чем больше энтропия, тем более неупорядоченное состояние занимает система; чем меньше энтропия, тем меньше в системе хаоса и беспорядка, тем более организованной она является.
В физике показано, что энтропия также характеризует отклонение системы от равновесия. Равновесному состоянию системы соответствует максимум хаоса и беспорядка. Чем более упорядоченной (другими словами, более организованной) является система, тем дальше она удалена от равновесия. Все сказанное иллюстрирует рис. 2.3.
Теперь можно дать еще одну формулировку второго начала термодинамики: при любых процессах полная энтропия замкнутой системы либо увеличивается, либо остается постоянной. (Среди физиков бытует шутка, в которой энтропия сравнивается со старой властной теткой: ее все недолюбливают, но она всегда права.)
Ранее было доказано, что энтропия идеального газа есть параметр состояния. Используя теорему Карно и учение об обратимых циклах, т.е. на базе второго закона термодинамики, можно доказать, что энтропия любого реального тела есть параметр состояния.
Для доказательства этого утверждения рассмотрим в Р,v- диаграмме произвольный внутренне обратимый (без трения) цикл (рис.9.14 а), который совершает реальное рабочее тело. При этом цикл может быть внешне необратимым, в данном случае, наличие разности температур между рабочим телом и источникам теплоты, роли не играют. Разобьем наш цикл, расположенными бесконечно близко друг к другу, адиабатами 14, 23, и т.д. на бесконечно большое количество элементарных циклов. Каждый из этих циклов можно считать циклом Карно, поскольку отрезки, полученные при делении цикла адиабатами, при бесконечно большом количестве последних можно считать изотермами, т.е. отрезок 12 и отрезок 34 заменить изотермами и т.д..
Совокупность этих элементарных циклов Карно эквивалентна нашему циклу, поскольку подведенная и отведенная теплота, а соответственно и работы циклов, будут одинаковы. Таким образом, наш цикл можно рассматривать как сумму бесконечного числа таких элементарных циклов Карно.
Для каждого элементарного цикла Карно, не зависимо от свойств рабочего тела, можно записать выражение термического КПД в виде
где ∂q1 и ∂q2 - количество подведенной и отведенной теплоты;
Т1 и Т2 - температуры подвода и отвода теплоты цикла.
Из этого выражения получаются равенства
при этом последнее выражение записано с учетом того, что отведенная теплота ∂q2 не взята по модулю (как это сделано в выражении термического КПД), т.е. второе слагаемое этого выражения отрицательное.
Для совокупности всех элементарных циклов Карно, т.е. для всего замкнутого процесса, который совершает реальное рабочее тело можно записать выражение
что соответствует интегралу по замкнутому контуру для нашего цикла в виде.
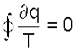Выражение (9.13) впервые было получено Клаузиусом и получило название интеграла Клаузиуса. Равенство нулю интеграла по замкнутому контуру свидетельствует о том, что под интегралом находится выражение полного диффиринциала. Выражение ∂q/T есть полный дифференциал энтропии, т.е. ∂q/T = ds, что позволяет записать выражение (9.13) в виде
Выражение (9.14) свидетельствует о том, что энтропия определяет состояние реального тела, т.е. она является параметром состояния любого реального тела. Следовательно, после этого доказательства принадлежности энтропии реальных тел к параметру состояния мы можем изобразить наш цикл в T,s- диаграмме (рис.9.14 б).
Понятия энтропии, связанной с механической, электрической или с любой энергией упорядоченного движения, в технической термодинамике не существует. Оно появляется только тогда, когда происходит превращение этих видов энергии в теплоту. То есть, есть теплота, есть и изменение энтропии. Являясь параметром состояния, энтропия, а точнее ее изменение, характеризует термодинамические процессы с точки зрения второго закона термодинамики.
Для обратимого процесса, используя первый закон термодинамики, изменение энтропии можно записать в виде выражения:
Для необратимого термодинамического процесса часть работы расширения за счет трения преобразуется в теплоту трения и усваивается телом. Поскольку в данном процессе будет присутствовать внешний и внутренний (за счет трения) подвод теплоты к телу, то и изменение энтропии (а, следовательно, и изменение термодинамического состояния тела) будет определяться как внешней теплотой, так и теплотой трения. Для необратимого термодинамического процесса изменение энтропии тела можно представить в виде выражения:
где ∂q = du + Pdv - ∂lтр = du + Pdv - ∂qтр - количество теплоты, полученное телом извне (внешняя теплота);
∂qтр = ∂lтр - количество теплоты, полученное телом за счет потерь работы расширения на трение (теплота трения);
∂q* = ∂q + ∂qтр = du + Pdv - полное количество теплоты, полученное телом (это выражение первого закона термодинамики для необратимого процесса).
Поскольку в реальном необратимом процессе теплота трения всегда величина положительная ∂qтр>0, то для необратимого процесса справедливо соотношение
Для обратимого процесса теплота трения отсутствует, что приводит к соотношению вида
Выражения (9.17) и (9.18) можно рассматривать как аналитические выражения второго закона термодинамики для тела, находящегося в замкнутой термодинамической системе.
Используя эти выражения, можно дать следующую формулировку второго закона термодинамики для тела - необратимость термодинамического процесса для тела приводит к увеличению изменения энтропии необратимого процесса по сравнению с изменением энтропии аналогичного обратимого процесса, при том же количестве подведенной внешней теплоты.
Такое увеличение энтропии тела для необратимого процесса, по сравнению с аналогичным обратимым, наглядно демонстрируется на примере адиабатных процессов
Адиабатные процессы широко используются в технике - процессы расширения газа или пара в турбине, сжатия воды в насосе или газа в компрессоре. Для обратимых процессов ∂q=0 и ds=0, т.е. обратимая адиабата является изоэнтропой (процессы 12 и 34). В реальных адиабатных процессах всегда происходит увеличение энтропии, обусловленное наличием трения. Так, для необратимых адиабатных процессов 12* и 34* возрастание энтропии на величину s2*-s2 и s4*-s3 соответственно, обусловлено только теплотой трения этих процессов.
В связи с тем, что выражение ∂q* = Tds* отражает второй закон термодинамики, объединив его с первым законом термодинамики можно получить объединенное уравнение первого и второго законов термодинамики в виде выражений
где ds - изменение энтропии для любого процесса, как обратимого, так и для необратимого (звездочку при энтропии здесь не указывают).
Выражения (9.19) и (9.20) справедливы для любых процессов: обратимых и необратимых. Эти выражения используются для анализа термодинамических процессов и являются исходными для дифференциальных уравнений термодинамики в частных производных.
Дата добавления: 2014-11-24; просмотров: 262 | Поможем написать вашу работу | Нарушение авторских прав |