Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Компоненты связности графа. Степень вершины. Теорема о сумме степеней вершин графа.

Компонента связности графа — некоторое множество вершин графа такое, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества.

Степень вершины (англ. degree, также валентность, англ. valency) в теории графов — количество рёбер графа , инцидентных вершине . При подсчёте степени ребро-петля учитывается дважды.^[1] Степень вершины обозначается как (в западных источниках — ). Максимальная и минимальная степень вершин графа G обозначаются соответственно Δ(G) и δ(G).

Сумма степеней всех вершин графа есть четное число, равное удвоенному количеству ребер

54 Полный граф; формула количества рёбер в полном графе.

Полный граф — простой граф, в котором каждая пара различных вершин смежна. Полный граф с вершинами имеет рёбер и обозначается . Является регулярным графом степени .

55 Алгоритм фронта волны в графе. Методика выделения компонент связности в графе.

алгоритм нахождения числа компонент связности, а также выделения этих компонент на неориентированном графе. Подобным образом решается задача и для ориентированного графа. В основу рассматриваемого алгоритма выделения компонент связности положена описанная ранее техника поиска в глубину на графе Г(X,U,Ф). Структура алгоритма. является модификацией в сторону упрощения основного алгоритма поиска в глубину. Работа алгоритма направлена на формирование вектора Mark[x] меток вершин x X графа. Элементу Mark[x] присваивается общий номер той компоненты, которой принадлежит вершина x X. Сложность алгоритма как и алгоритма составляет O(|X|+|U|).

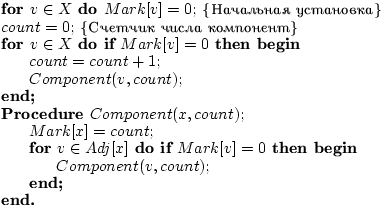
56 Мосты и разделяющие вершины (точки сочленения).

Вершину зовут разделяющей, если ее удаление увеличивает число компонент графа; ребро, обладающее этим свойством, зовут мостом. Как правило, вершины, инцидентные мосту, являются разделяющими за исключением, если одна из вершин ребра является концевой.
Теорема: вершина V графа является разделяющей, если существуют такие две вершины, что любая цепь, их соединяющая, проходит через вершину V

Точка сочленения графа — вершина графа , при удалении которой граф имеет большекомпонент связности, чем исходный граф .