Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Электромагнетизм

8. Эффект Холла.

Эффект Холла* (1879) — это возникновение в металле (или полупроводнике) с током плотностью j, помещенном в магнитное поле В, электрического поля в направлении, перпендикулярном В и j.

* Э. Холл (1855—1938) — американский физик.

Поместим металлическую пластинку с током плотностью j в магнитное поле В, перпендикулярное j (рис. 172). При данном направлении j скорость носителей тока в металле — электронов — направлена справа налево. Электроны испытывают дейст­вие силы Лоренца (см. § 114), которая в данном случае направлена вверх. Таким образом, у верхнего края пластинки возникнет повышенная концентрация электронов (он зарядится отрицательно), а у нижнего — их недостаток (зарядится положительно). В результате этого между краями пластинки возникнет дополнительное поперечное электрическое поле, направленное снизу вверх. Когда напряженность Е_B этого попереч­ного поля достигнет такой величины, что его действие на заряды будет уравновеши­вать силу Лоренца, то установится стационарное распределение зарядов в поперечном направлении. Тогда

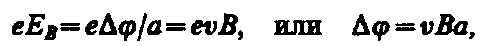
где а — ширина пластинки, Dj — поперечная (холловская) разность потенциалов.

Учитывая, что сила тока I=jS=nevS (S — площадь поперечного сечения пластинки толщиной d, п — концентрация электронов, v — средняя скорость упорядоченного движения электронов), получим

(117.1)

т. е. холловская поперечная разность потенциалов прямо пропорциональна магнитной индукции В, силе тока I и обратно пропорциональна толщине пластинки d. В формуле (117.1) R= 1 / (en) — постоянная Холла, зависящая от вещества. По измеренному значе­нию постоянной Холла можно: 1) определить концентрацию носителей тока в провод­нике (при известных характере проводимости и заряда носителей); 2) судить о природе проводимости полупроводников (см. § 242, 243), так как знак постоянной Холла совпадает со знаком заряда е носителей тока. Эффект Холла поэтому — наиболее эффективный метод изучения энергетического спектра носителей тока в металлах и полупроводниках. Он применяется также для умножения постоянных токов в анало­говых вычислительных машинах, в измерительной технике (датчики Холла) и т. д.

8.Ускорители заряженных частиц.

Ускорителями заряженных частиц называются устройства, в которых под действием электрических и магнитных полей создаются и управляются пучки высокоэнергетичных заряженных частиц (электронов, протонов, мезонов и т. д.).

Любой ускоритель характеризуется типом ускоряемых частиц, энергией, сообща­емой частицам, разбросом частиц по энергиям и интенсивностью пучка. Ускорители делятся на непрерывные (из них выходит равномерный по времени пучок) и импульсные (из лих частицы вылетают порциями — импульсами). Последние характеризуются длительностью импульса. По форме траектории и механизму ускорения частиц ускори­тели делятся на линейные, циклические и индукционные. В линейных ускорителях траектории движения частиц близки к прямым линиям, в циклических и индукцион­ных — траекториями частиц являются окружности или спирали.

Рассмотрим некоторые типы ускорителей заряженных частиц.

1. Линейный ускоритель. Ускорение частиц осуществляется электростатическим полем, создаваемым, например, высоковольтным генератором Ван-де-Граафа (см. § 92). Заряженная частица проходит поле однократно: заряд Q, проходя разность потенциалов j₁—j₂, приобретает энергию W=Q (j₁—j₂). Таким способом частицы ускоряются до»10 МэВ. Их дальнейшее ускорение с помощью источников постоян­ного напряжения невозможно из-за утечки зарядов, пробоев и т. д.

2. Линейный резонансный ускоритель. Ускорение заряженных частиц осуществляет­ся переменным электрическим полем сверхвысокой частоты, синхронно изменяющимся с движением частиц. Таким способом протоны ускоряются до энергий порядка десят­ков мегаэлектрон-вольт, электроны — до десятков гигаэлектрон-вольт.

3. Циклотрон — циклический резонансный ускоритель тяжелых частиц (протонов, ионов). Его принципиальная схема приведена на рис. 171. Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода (1 и 2) в виде полых металлических полуцилиндров, или дуантов. К дуантам приложено переменное электрическое поле. Магнитное поле, создаваемое электромагнитом, одно­родно и перпендикулярно плоскости дуантов.

Если заряженную частицу ввести в центр зазора между дуантами, то она, ускоря­емая электрическим и отклоняемая магнитным полями, войдя в дуант 1, опишет полуокружность, радиус которой пропорционален скорости частицы (см. (115.1)). К моменту ее выхода из дуанта 1 полярность напряжения изменяется (при соответст­вующем подборе изменения напряжения между дуантами), поэтому частица вновь ускоряется и, переходя в дуант 2, описывает там уже полуокружность большего радиуса и т. д.

Для непрерывного ускорения частицы в циклотроне необходимо выполнить условие синхронизма (условие «резонанса») — периоды вращения частицы в магнитном поле и колебаний электрического поля должны быть равны. При выполнении этого условия частица будет двигаться по раскручивающейся спирали, получая при каждом прохож­дении через зазор дополнительную энергию. На последнем витке, когда энергия частиц и радиус орбиты доведены до максимально допустимых значений, пучок частиц посредством отклоняющего электрического поля выводится из циклотрона.

Циклотроны позволяют ускорять протоны до энергий примерно 20 МэВ. Даль­нейшее их ускорение в циклотроне ограничивается релятивистским возрастанием мас­сы со скоростью (см. (39.1)), что приводит к увеличению периода обращения (по (115.2) он пропорционален массе), и синхронизм нарушается. Поэтому циклотрон совершенно неприменим для ускорения электронов (при E =0,5 МэВ m =2 m ₀, при E =10 МэВ m =28 m ₀ !).

Ускорение релятивистских частиц в циклических ускорителях можно, однако, осу­ществить, если применять предложенный в 1944 г. В. И. Векслером (1907—1966) и в 1945 г. американским физиком Э. Мак-Милланом (р. 1907) принцип автофазировки. Его идея заключается в том, что для компенсации увеличения периода вращения частиц, ведущего к нарушению синхронизма, изменяют либо частоту ускоряющего электрического, либо индукцию магнитного полей, либо то и другое. Принцип автофазировки используется в фазотроне, синхротроне и синхрофазотроне.

4. Фазотрон (синхроциклотрон) — циклический резонансный ускоритель тяжелых заряженных частиц (например, протонов, ионов, a -частиц), в котором управляющее магнитное поле постоянно, а частота ускоряющего электрического поля медленно изменяется с периодом. Движение частиц в фазотроне, как и в циклотроне, происходит по раскручивающейся спирали. Частицы в фазотроне ускоряются до энергий, примерно равных 1 ГэВ (ограничения здесь определяются размерами фазотрона, так как с ро­стом скорости частиц растет радиус их орбиты).

5. Синхротрон — циклический резонансный ускоритель ультрарелятивистских элек­тронов, в котором управляющее магнитное поле изменяется во времени, а частота ускоряющего электрического поля постоянна. Электроны в синхротроне ускоряются до энергий 5—10 ГэВ.

6. Синхрофазотрон — циклический резонансный ускоритель тяжелых заряженных частиц (протонов, ионов), в котором объединяются свойства фазотрона и синхротрона, т. е. управляющее магнитное поле и частота ускоряющего электрического поля одно­временно изменяются во времени так, чтобы радиус равновесной орбиты частиц оставался постоянным. Протоны ускоряются в синхрофазотроне до энергий 500 ГэВ.

7. Бетатрон — циклический индукционный ускоритель электронов, в котором уско­рение осуществляется вихревым электрическим полем (см. § 137), индуцируемым переменным магнитным полем, удерживающим электроны на круговой орбите. В бета­троне в отличие от рассмотренных выше ускорителей не существует проблемы синхро­низации. Электроны в бетатроне ускоряются до энергий 100 МэВ. При W > 100 МэВ режим ускорения в бетатроне нарушается электромагнитным излучением электронов. Особенно распространены бетатроны на энергии 20—50 МэВ.

8. Э.д.с. индукции – закон Фарадея.

Обобщая результаты своих многочисленных опытов, Фарадей пришел к количествен­ному закону электромагнитной индукции. Он показал, что всякий раз, когда проис­ходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электро­магнитной индукции. Значение индукционного тока, а следовательно, и э.д.с. электро­магнитной индукции определяются только скоростью изменения магнитного потока, т. е.

Теперь необходимо выяснить знак . В § 120 было показано, что знак магнитного потока зависит от выбора положительной нормали к контуру. В свою очередь, положительное направление нормали определяется правилом правого винта (см. § 109). Следовательно, выбирая положительное направление нормали, мы определяем как знак потока магнитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими представлениями и выводами, можно соответственно прийти к форм­улировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим кон­туром, возникающая в контуре э. д. с.

(123.2)

Знак минус показывает, что увеличение потока вызывает э. д. с. т. е. поле индукционного тока направлено навстречу потоку; уменьшение потока вызывает т.е. направления потока и поля индукционного тока совпадают. Знак минус в формуле (123.2) определяется правилом Ленца — общим правилом для нахождения направления индукционного тока, выведенного в 1833 г.

Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызва­вшему этот индукционный ток.

Закон Фарадея (см. (123.2)) может быть непосредственно получен из закона со­хранения энергии, как это впервые сделал Г. Гельмгольц. Рассмотрим проводник с током I, который помещен в однородное магнитное поле, перпендикулярное плоско­сти контура, и может свободно перемещаться (см. рис. 177). Под действием силы Ампера F, направление которой показано на рисунке, проводник перемещается на отрезок d x. Таким образом, сила Ампера производит работу (см. (121.1)) d A = I dФ, где dФ — пересеченный проводником магнитный поток.

Согласно закону сохранения энергии, работа источника тока за время d t () будет складываться из работы на джоулеву теплоту (I ² R d t) и работы по перемещению проводника в магнитном поле (I dФ):

где R — полное сопротивление контура. Тогда

= есть не что иное, как закон Фарадея (см. (123.2)).

Закон Фарадея можно сформулировать еще таким образом: э.д.с. электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: э. д. с. не зависит от способа изменения магнитного потока. Э.д.с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим

Какова природа э.д.с. электромагнитной индукции? Если проводник (подвижная перемычка контура на рис. 177) движется в постоянном магнитном поле, то сила Лоренца, действующая на заряды внутри проводника, движущиеся вместе с проводни­ком, будет направлена противоположно току, т. е. она будет создавать в проводнике индукционный ток противоположного направления (за направление электрического тока принимается движение положительных зарядов). Таким образом, возбуждение э.д.с. индукции при движения контура в постоянном магнитном поле объясняется действием силы Лоренца, возникающей при движении проводника.

Согласно закону Фарадея, возникновение э.д.с. электромагнитной индукции воз­можно и в случае неподвижного контура, находящегося в переменном магнитном поле. Однако сила Лоренца на неподвижные заряды не действует, поэтому в данном случае ею нельзя объяснить возникновение э.д.с. индукции. Максвелл для объяснения э.д.с. индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция вектора Е _B этого поля по любому неподвижному контуру L проводника представляет собой э. д. с. электромагнитной индукции:

(123.3)

8. Магнитная проницаемость вещества.

Подобно тому, как для количественного описания поляризации диэлектриков вводи­лась поляризованность (см. § 88), для количественного описания намагничения магнетиков вводят векторную величину — намагниченность, определяемую магнитным моментом единицы объема магнетика:

где — магнитный момент магнетика, представляющий собой векторную сумму магнитных моментов отдельных молекул (см. (131.6)).

Рассматривая характеристики магнитного поля (см. § 109), мы вводили вектор магнитной индукции В, характеризующий результирующее магнитное поле, создава­емое всеми макро- и микротоками, и вектор напряженности Н, характеризующий магнитное поле макротоков. Следовательно, магнитное поле в веществе складывается из двух полей: внешнего поля, создаваемого током, и поля, создаваемого намагничен­ным веществом. Тогда можем записать, что вектор магнитной индукции результирующего магнитного ноля в магнетике равен векторной сумме магнитных индукций внешнего поля В ₀ (поля, создаваемого намагничивающим током в вакууме) и поля микротоков В ' (поля, создаваемого молекулярными токами):

(133.1)

где В ₀= m ₀ Н (см. (109.3)).

Для описания поля, создаваемого молекулярными токами, рассмотрим магнетик в виде кругового цилиндра сечения S и длины l, внесенного в однородное внешнее магнитное поде с индукцией В ₀. Возникающее в магнетике магнитное поле молекуляр­ных токов будет направлено противоположно внешнему полю для диамагнетиков и совпадать с ним по направлению для парамагнетиков. Плоскости всех молекулярных токов расположатся перпендикулярно вектору В ₀, так как векторы их магнитных моментов p _m антипараллельны вектору В ₀ (для диамагнетиков) и параллельны В ₀ (для парамагнетиков). Если рассмотреть любое сечение цилиндра, перпендикулярное его оси, то во внутренних участках сечения магнетика молекулярные токи соседних атомов направлены навстречу друг другу и взаимно компенсируются (рис. 189). Нескомпенсированными будут лишь молекулярные токи, выходящие на боковую поверхность цилиндра.

Ток, текущий по боковой поверхности цилиндра, подобен току в соленоиде и созда­ет внутри него поле, магнитную индукцию В' которого можно вычислить, учитывая формулу (119.2) для N = 1 (соленоид из одного витка):

(133.2)

где I' — сила молекулярного тока, l — длина рассматриваемого цилиндра, а магнит­ная проницаемость m принята равной единице.

С другой стороны, I'/l — ток, приходящийся на единицу длины цилиндра, или его линейная плотность, поэтому магнитный момент этого тока p = I'lS/l = I'V/l, где V — объем магнетика. Если Р — магнитный момент магнетика объемом V, то намаг­ниченность магнетика

(133.3)

Сопоставляя (133.2) и (133.3), получим, что

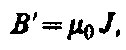
или в векторной форме

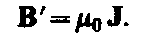
Подставив выражения для В ₀ и В' в (133.1), получим

(133.4)

или

(133.5)

Как показывает опыт, в несильных полях намагниченность прямо пропорциональ­на напряженности поля, вызывающего намагничение, т. е.

(133.6)

где c — безразмерная величина, называемая магнитной восприимчивостью вещества. Для диамагнстихов c отрицательна (поле молекулярных токов противоположно вне­шнему), для парамагнетиков — положительна (поле молекулярных токов совпадает с внешним).

Используя формулу (133.6), выражение (133.4) можно записать в виде

(133.7)

откуда

Безразмерная величина

(133.8)

представляет собой магнитную проницаемость вещества. Подставив (133.8) в (133.7), придем к соотношению (109.3) В = m ₀ m Н, которое ранее постулировалось.

Так как абсолютное значение магнитной восприимчивости для диа- и парамаг­нетиков очень мало (порядка 10^–4 —10^–6), то для них m незначительно отличается от единицы. Это просто понять, так как магнитное поле молекулярных токов значительно слабее намагничивающего поля. Таким образом, для диамагнетиков c<0 и m <1, для парамагнетиков c>0 и m >1.

Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора В) является обобщением закона (118.1):

где I и I' — соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым кон­туром L. Таким образом, циркуляция вектора магнитной индукции В по произволь­ному замкнутому контуру равна алгебраической сумме токов проводимости и молеку­лярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. Вектор В, таким образом, характеризует результирующее поле, созданное как мак­роскопическими токами в проводниках (токами проводимости), так и микроскопичес­кими токами в магнетиках, поэтому линии вектора магнитной индукции В не имеют источников и являются замкнутыми.

Из теории известно, что циркуляция намагниченности J по произвольному замкну­тому контуру L равна алгебраической сумме молекулярных токов, охватываемых этим контуром:

Тогда закон полного тока для магнитного поля в веществе можно записать также в виде

(133.9)

где I, подчеркнем это еще раз, есть алгебраическая сумма токов проводимости.

Выражение, стоящее в скобках в (133.9), согласно (133.5), есть не что иное, как введенный ранее вектор H напряженности магнитного поля. Итак, циркуляция вектора Н по произвольному замкнутому контуру L равна алгебраической сумме токов проводимости, охватываемых этим контуром:

(133.10)

Выражение (133.10) представляет собой теорему о циркуляции вектора Н.