Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Электромагнетизм

23. Магни́тное поле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения, магнитная составляющая электромагнитного поля.

24. Магни́тная инду́кция — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .

Более конкретно, — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля на заряд , движущийся со скоростью , равна

где α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).

25. Принцип суперпозиции может быть сформулирован так: Магнитное поле, создаваемое несколькими токами, есть векторная сумма полей, которые бы создавались каждым из этих токов по отдельности.Или напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумманапряженностей полей отдельных зарядов.

26.магнитное поле движущего заряда (формула): где r — радиус-вектор, проведенный от заряда Q к данной точке.Вектор В направлен перпендикулярно плоскости, в кото­рой расположены векторы v и r, а именно: его направление совпадает с направлением поступательного движения правого винта при его вращении от v к r.

27. Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током. Лаплас показал также, что с помощью этого закона можно вычислить магнитное поле движущегося точечного заряда (считая движение одной заряженной частицы током).

28. Силу, действующую со стороны магнитного поля на движущиеся в нем заряды, называют силой Лоренца. Сила Лоренца определяется соотношением: Fл = q·V·B·sinα

где q - величина движущегося заряда;

V - модуль его скорости;

B - модуль вектора индукции магнитного поля;

a - угол между вектором скорости заряда и вектором магнитной индукции.

29. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Модуль силы Ампера можно найти по формуле:

30.Магнитный момент контура с током- это вектор, направленный в зависимости от направления тока, если ток течёт в замкнутом контуре по часовой стрелке,то момент будет направлен вниз из центра контура, ну и численно от равен величине тока на площадь контура. ,

31. Если в однородном магнитном поле помещен плоский контур прямоугольной формы с током, то на него действует пара сил, стремящихся повернуть контур вокруг оси. Вращающий момент этой пары сил равен произведению величины одной из сил на расстояние (плечо) между токами приложения этих сил.

32. Энергия магнитного поля системы n контуров с токами равна полусумме произведений токов в контурах на потокосцепление контуров 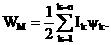Так, энергия магнитного поля одного контура или катушки с током определяется (с учетом выражения следующим образом: Энергия системы двух контуров, связанных друг с другом посредством магнитного поля, равна

33. Работа, совершаемая проводником с током при перемещении,- численно равна произведению тока на магнитный поток, пересечённый этим проводником.

34. Теорема Гаусса для магнитной индукции:

Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.

Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле[5]. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является (полностью) вихревым.

Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

35. Циркуляция вектора напряженности — циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме макроскопических токов, охватываемых этим контуром.

36. Явление электромагнитной индукции - говорит о том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного.

Закон Фарадея гласит: Для любого замкнутого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур.

37. Самоиндукция — возникновение ЭДС индукции в замкнутом проводящем контуре[1] при изменении тока, протекающего по контуру.

38. Энергия магнитного поля. Плотность энергии магнитного поля.

Энергия магнитного поля совпадает с работой контура,

затрачиваемой током на создание этого поля

Энергия магнитного поля, которое связано с контуром:

Плотность энергии магнитного поля:

Неоднородного -

39. Уравнение Максвелла - система дифференциальных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сложных средах.

Интегральная форма:

а) Закон Гаусса

Поток электрической индукции через замкнутую поверхность S пропорционален величине свободного заряда, находящегося в объёме V, который окружает поверхность S.

б) Закон Гаусса для магнитного поля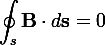

Поток магнитной индукции через замкнутую поверхность равен нулю (магнитные заряды не существуют).

в) Закон индукции Фарадея

Изменение потока магнитной индукции, проходящего через незамкнутую поверхность S, взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре L, который является границей поверхности S.

г) Теорема о циркуляции магнитного поля

Полный электрический ток свободных зарядов и изменение потока электрической индукции через незамкнутую поверхность S, пропорциональны циркуляции магнитного поля на замкнутом контуре L, который является границей поверхности S.

– электрический заряд в объеме V,ограниченной поверхностью S. – электрический ток проходит через поверхность S.

40. а) Ферромагнетики- такое вещество, которое, при температуре ниже точки Кюри, способно обладать намагниченностью в отсутствие внешнего магнитного поля.

Свойства: Магнитная восприимчивость ферромагнетиков положительна и значительно больше единицы. При не слишком высоких температурах ферромагнетики обладают самопроизвольной (спонтанной) намагниченностью, которая сильно изменяется под влиянием внешних воздействий. Для ферромагнетиков характерно явление гистерезиса.(Fe,Ca,Ni,Al)

б) Парамагнетики- вещества, которые намагничиваются во внешнем магнитном поле в направлении внешнего магнитного поля. Парамагнетики относятся к слабомагнитным веществам, магнитная проницаемость незначительно отличается от единицы .(Al, ,NO)

в) Диамагнетики- вещества, намагничивающиеся против направления внешнего магнитного поля. В отсутствие внешнего магнитного поля диамагнетики немагнитны. Под действием внешнего магнитного поля каждый атом диамагнетика приобретает магнитный момент I, пропорциональный магнитной индукции H и направленный навстречу полю. ( Ge Si)

41. Волна, типа , где - волновой вектор, называется плоской (можно писать в скалярной форме, т.к. все одинаково для магнитных и электрических полей).

42. Плоская электромагнитная волна- электромагнитная волна, в которой всем точкам, лежащим в любой плоскости, перпендикулярной направлению ее распространения, соответствуют одинаковые напряженности электрических или магнитных полей.

Как известно, электромагнитные поля определяются путём задания в каждой точке пространства четырёх векторов:

а) вектора напряжённости электрического поля;(вектор E)

б) вектора напряжённости магнитного поля;(вектор H)

в) вектора электрического смещения;(вектор D)

г) вектора магнитной индукции.(вектор B)

43. Энергия электромагнитной волны внутри некоторого объема определяется плотностью энергии электромагнитного поля волны: Плотность энергии электромагнитного поля – физическая величина равная отношению энергии электромагнитного поля в некотором объеме к величине этого объема.