
Читайте также:
|
Многообразие взаимосвязей в которых находятся социально-экономические явления, рождают необходимость в их классификации.
По видам различают функциональную и корреляционную зависимость.
Функциональной называют такую зависимость, при которой одному значению факторного признака X соответствует одно строго определенное значение результативного признака Y.
В отличие от функциональной зависимости, корреляционная выражает такую связь между социально-экономическими явлениями, при которой одному значению факторного признака X могут соответствовать несколько значений результативного признака Y.
По направлению различают прямую и обратную зависимость.
Прямой называют такую зависимость, при которой значение факторного признака X и результативного признака Y изменяются в одном направлении. Т.о. при увеличении значения X, значения Y в среднем увеличиваются, а при уменьшении X - Y уменьшается.
Обратная зависимость между факторным и результативным признаками, если они изменяются в противоположных направлениях.
Билет 33 Причинность, регрессия, корреляция. Для количественного описания взаимосвязей между экономическими переменными в статистике используют методы регрессии и корреляции. Регрессия - величина, выражающая зависимость среднего значения случайной величины у от значений случайной величины х. Уравнение регрессии выражает среднюю величину одного признака как функцию другого. Корреляция- величина, отражающая зависимости средней величины одного признака от изменения значения другого признака.
Билет 34 Уравнение регрессии, определение его параметров.
В модели регрессионого анализа характеристкой статистической связи теоретическая линия регрессии, которая описывается функцией у=f(x), которая называется уравнением регрессии: yср(x)=f(x)
Уравнение регрессии может быть парным если изучаетчя связь между y и х и может быть множественным если изучаетчя зависимость между у и большим числом факторных признаков х
Для изучения зависимости между у и х применяется различные уравнения
Само уравнение регрессии показывает как и на сколько в среднем увеличивается (уменьшается) результативны признак с увеличением (уменьшением) факторного на 1, в этом случае если признак факторный изменяется в арифметической прогрессии а результативный увеличивается по геометрической, в качестве уравнения связи выбирается парабола, если связь обратная то гипербола, тоесть нелинейные уравнения применяются тогда, когда изменения взаимосвязанных признаков происходят неравномерно(с ускорением, замедлением или с переменным направлением связи)
Билет 35 Определение тесноты корреляционной связи. При изучении корреляционной связи важным направлением анализа является оценка степени тесноты связи. Понятие степени тесноты связи между двумя признаками возникает вследствие того, что в реальной действительности на изменение результативного признака влияют несколько факторов. При этом влияние одного из факторов может выражаться более заметно и четко, чем влияние других факторов. С изменением условий в качестве главного, решающего фактора может выступать другой. Показатели тесноты связи должны удовлетворять ряду основных требований: 1) величина показателя степени тесноты связи должна быть равна или близка к нулю, если связь между изучаемыми признаками (процессами, явлениями) отсутствует; 2) при наличии между изучаемыми признаками (х и у) функциональной связи величина степень тесноты связи равна единице; 3) при наличии между признаками (х и у) корреляционной связи показатель тесноты связи выражается правильной дробью, которая по величине тем больше, чем теснее связь между изучаемыми признаками (стремится к единице)
Билет 36 Анализ взаимосвязей качественных признаков
Для исследования взаимосвязи качественных альтернативных признаков, принимающих только 2 взаимоисключающих значения, используется коэффициент ассоциации и контингенции. При расчете этих коэффициентов составляется т.н. таблица 4-х камней, а сами коэффициенты рассчитываются по формуле:
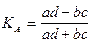

Билет 37 Понятие ряда динамики. Виды динамических рядов. Ряды динамики- это числовые значения определенного стат. показателя в последовательные моменты или периоды времени (т.е расположенные в хронологическом порядке) Виды: по времени- ряды моментальные и интервальные, которые показывают уровень явления на конкретный момент времени или на пределенный период времени. По форме представления- ряды абсолютные, относительных и средних велечин. По интервалам времени- ряды равномерные и неравномерные, первые из которых имеют равные интервалы, а у вторых равенство интервалов не соблюдается По числу смысловых стат. величин- ряды изолированные и комплексные. Первые представляют собой ряд динамики одной стат. величины, а вторые- нескольких.
Билет 38 Аналитические показатели ряда динамики.
38. Аналитические показатели изменения уровня ряда динамики
Анализ скорости интенсивности развития явления во времени осуществляется с помощью Аналитических показателей, которые получаются в результате сравнении уровней между собой
Показатели абсолютной скорости и интесивности развития рядов динамики Абсолютный прирост - характеризует размер, увеличения или уменьшения уровня ряда за определенный момент времени. Обозгачается через Дельта и представляет с собой разность двух сравниваемых уровней. Эта разность выражает абсолютную скорость роста. Абсолютный прирост может вычислятся как цепной так и базисный. Цепной означает переменную базу сравнения
Базисные - постоянные. Принимается либо 1ый (у1)уровень либо уровень заданный бав сравненияи(у0) В целом за период вычисляется средний абсолютный прирост Скоростью в данном случае будем называть прирост(уменьшение) в единицу времени. Первая формула поменяется в том случае если у нас есть цепные абсолютные приросты и их сумма Вторая формула если нет расчета цепных абсолютных приростов а есть первый и последний уровень ряда Yn - последний уровень ряда а y1 первый или начальный Абсолютный прирост имеет туже единицу измерения что и уровни ряда Интенсивность изменения уровня ряда оценивается отношением отчетного уровня к базисному, который всегда представляет с собой положительное число, тоесть выраженое либо в коэффициентах либо в процентах Показатель интенсивности изменения уровня ряда называется коэффициентом роста или темпом роста. В коэф база сравнения единица а в темпах сто. Коэффициент роста показывает во сколько раз данный уровень ряда больше базисного. Или на какую часть базисного уровня составляет текущего периода за некоторый промежуток времени(если он меньше 1) Кр*100% = Тр Коэффициент роста в анализе используется в том случае, если числитель больше знаменателя более чем в два раза Темп роста вычисляется когда числитель больше чем знаменатель менее чем в два раза Темпы роста могут быть как цепные так и базисные Цепной темп роста(с переменной базой)
Базисные (с постоянной базой) Между цепными и базисными темпами роста существует Взаимосвязь Произведение всех цепных Тр равно конечному басизнуму Деление последующего цепного абсолютного прироста на предыщй дает соответствующий базисный коэффициент роста
Темп прироста Характеризует на сколько процентов увеличился или уменьшился текущий уровень ряда по сравнению с базисным
Темп роста показывает сколько в среднем процентов последующий уровень составляет от предыдущего в течении всего Периода наблюдения
Абсолютное значение одного процента прироста В реальной экономике часто расчитывается. Этот показатель показывает замедлением темпов прироста (ускорение). В относительных велечинами не всегда сопроваждается уменьшением или возрастанием абсолюытных приростов. Абсолютный прирост поедставляет собой 1/100 предыщего уровня и расчитывается в тех же единицах измер
Билет 39 Аналитические показатели изменения уровней ряда динамики. Базисные показатели характеризуют итоговый результат всех изменений в уровнях ряда от периода базисного уровня до данного периода. Цепные показатели характризуют интенсивность изменения уровня от одного периода к другому в пределах того промежутка времени, который исследуется. Абсолютный прирост- выражает абсолютную скорость изменения ряда динамики и определяется как разность между данным уровнем и уровнем, принятым за базу сравнения. Дельта а (б) = уi-yо Коэффицент роста определяется как отношение данного уровня к предыдущему или базисному, показывает относительную скорость изменения ряда. Ki=yi/yo Темп роста Tp=Kx100% Темп прироста определяется как отношение абсолютного прироста данного уровня к предыдущему или базисному Tn=yi-yi-1/yox100%
Дата добавления: 2015-01-30; просмотров: 103 | Поможем написать вашу работу | Нарушение авторских прав |