Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

OТРЫВ ПОГРАНИЧНОГО СЛОЯ ПРИ ОБТЕКАНИИ ТВЕРДЫХ ПОВЕРХНОСТЕЙ ГАЗОДИНАМИЧЕСКИМ ПОТОКОМ

В 1904 г. Л. Прандтль в своем докладе «О движении жидкости при очень малом трении», прочитанном на математическом конгрессе в Гейдельберге, указал путь, сделавший доступным теоретическому исследованию течения жидкости с трением в практически важных случаях. А именно, исходя из теоретических соображений и некоторых простых экспериментов, Л. Прандтль показал, что течение в окрестности тела можно разделить на две области: на область очень тонкого слоя вблизи тела (пограничный слой), где трение играет существенную роль, и на область вне этого слоя, где трением можно пренебрегать. Эта гипотеза, с одной стороны, позволила получить физически очень наглядное объяснение важной роли вязкости в проблеме сопротивления, а с другой стороны, дала возможность преодолеть математические трудности и тем самым открыла путь теоретическому исследованию течений жидкости с трением.

Плоское течение около тонкого клина при очень малой вязкости среды (очень большое число Рейнольдса)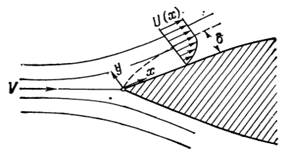

Обозначим величины:

u -продольная скорость(вдоль оси х);

v- поперечная скорость (вдоль оси у);

U- скорость внешнего потока;

V- скорость набегающего потока;

δ- толщина пограничного слоя;

L- характерный линейный размер тела

В течении будем рассматривать 2 области:

— Первая область - очень тонкий слой в непосредственной близости от тела. В этой области градиент скорости ∂u/∂y в направлении, перпендикулярном к стенке, очень велик, а вязкость μ оказывает существенное влияние на течение, поскольку здесь касательное напряжение τ= μ ∂u/∂y, вызванное трением, может принимать большие значения

— Вторая область-все остальное течение вне пограничного слоя. В этой области градиент скорости не достигает таких больших значений, как в пограничном слое, поэтому действие вязкости здесь не играет роли и можно считать, что течение здесь потенциальное.

Запишем уравнения Навье-Стокса в безразмерной форме, для этого:

— все скорости отнесем к скорости V набегающего потока;

— все длины –к характерному линейному размеру тела L,который выберем так, чтобы безразмерная величина ∂u/∂x в рассматриваемой области течения не превышала по порядку единицу;

— давление и время разделим соответственно на ρV² и на L/V;

— введем число Рейнольдса Re=VL/ν

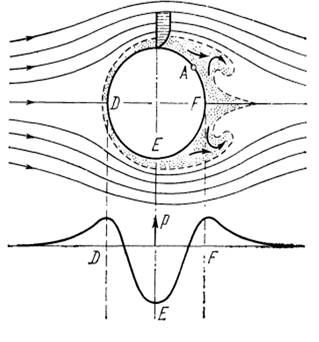
Схематическое изображение отрыва пограничного слоя и образования вихрей при обтекании круглого цилиндра; А-точка отрыва.

Критерии отрыва пограничного слоя:

Параметры, определяющие течение:

• U – скорость;

• ρ – плотность;

• Р – давление внешнего потока в сечении х^*;

• Р́_х (х^*);

• z- характерный размер пограничного слоя,

• μ – характерная const вязкости;

• λ – const теплопроводности;

• γ – отношение теплоёмкостей.

Характерным линейным размером пограничного слоя может быть δ, δ^*, δ^** и др.

- толщина вытеснения

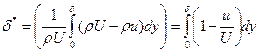
- толщина потери импульса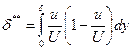

По теореме размерностей все безразмерные величины есть функции только безразмерных комбинаций определяющих параметров

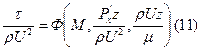
В точке отрыва пограничного слоя τ=0, т.е Ф=0, следовательно, соотношение (11) можно разрешить относительно параметра

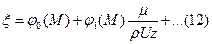Разложим функцию φ по 1/Re_z:

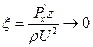Совершим предельный переход μ→0.
В ламинарном пограничном слое при μ→0, Re→∞, z→0.
Следовательно,

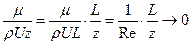Известно, что z/L~(Re)^-1/2 (Re=ρUL/μ), следовательно

T.к. φ₀(М) не стремится к 0 при μ→0, то для ламинарного пограничного слоя φ₀(М) ≡0.

Умножая обе части равенства (12) на ρUz/μ и переходя к пределу при Re→∞, получим, что в точке отрыва ламинарного пограничного слоя справедливо соотношение:

В случае турбулентного пограничного слоя при μ→0 характерный размер пограничного слоя z не стремится к 0 (т.к.толщина пограничного слоя определяется турбулентным перемешиванием). Следовательно, не стремится к 0 и Р́_хz/ρU². Поэтому в случае турбулентного пограничного слоя φ₀(М)≠0. Все остальные члены в (12) содержат Re^-1. Устремляя μ→0 (Re→∞), получим для турбулентного пограничного слоя над точкой отрыва соотношение: