Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Вычисление расстояния между параллельными плоскостями

Первый способ

Выберем любую точку на первой плоскости.

Применим формулу расстояния от точки до плоскости.

d=

Пример (Клетеник № 964(5)):

Вычислить расстояние между параллельными плоскостями:

30x-32y+24z-75=0 15x-16y+12z-25=0

Решение:

Пусть y=0 и z=0. Тогда подставив эти значения в первое уравнение, получим

x=2,5. Мы получили точку М(2,5; 0; 0). Применим формулу расстояния от точки до плоскости: d= 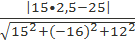=0,5

Ответ: 0,5

Второй способ

Если плоскость α задана уравнением Ax + By + Cz + D₁=0, а плоскость β задана уравнением Ax + By + Cz + D₂=0, то расстояние между параллельными плоскостями находим по следующей формуле:

d=

Пример(Клетеник №964(6)):

Вычислить расстояние между параллельными плоскостями:

6x-18y-9z-28=0 4x-12y-6z-7=0

Решение:

Умножив обе части второго уравнения на , получим 6x-18y-9z-10,5=0.

Применим формулу: d= =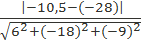

Ответ:

Вычисление расстояния от точки до прямой в пространстве