Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Нормальная составляющая ускорения

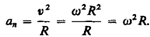
Основое уравнение динамики вращательного движения материальной точки - угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.

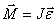
Taк как вектор скорости направлен по касательной к траектории, то вектор Dv _n, перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная

называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением).

Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис.5):

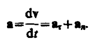
Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная состав­ляющая ускорения — быстроту изменения скорости по направлению (направлена к цен­тру кривизны траектории).

В зависимости от тангенциальной и нормальной составляющих ускорения движе­ние можно классифицировать следующим образом:

1) 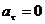, а_n = 0 — прямолинейное равномерное движение;

2) , а_n = 0 — прямолинейное равнопеременное движение. При таком виде движения

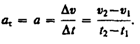
Если начальный момент времени t ₁=0, а начальная скорость v ₁ =v ₀, то, обозначив t ₂ =t и v ₂ =v, получим 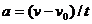, откуда

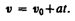
Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t, найдем, что длина пути, пройденного точкой, в случае равнопеременного движения

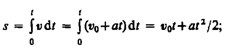
3) 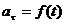, а_n = 0— прямолинейное движение с переменным ускорением;

4) 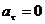, а_n = const. При 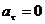скорость по модулю не изменяется, а изменяется по направлению. Из формулы a_n=v ² /r следует, что радиус кривизны должен быть посто­янным. Следовательно, движение по окружности является равномерным;

5) 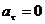, 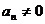— равномерное криволинейное движение;

6) 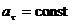, 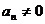— криволинейное равнопеременное движение;

7) 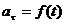, 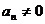— криволинейное движение с переменным ускорением.

Понятно, что линейные и соответствующие им угловые величины должны быть определенным образом связаны между собой. Найдем эти связи.

При повороте радиуса, проведенного в точку М (см. рис. 2), на угол φ точка пройдет по дуге окружности путь

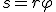. (1)

За малое время Δt точка проходит расстояние 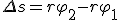, где φ2 и φ1 — углы поворота в конце и в начале интервала Δt. Разделив последнее равенство на Δt и учитывая, что 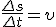и 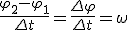, получим

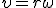. (2)

Заметим, что соотношение (2) связывает между собой линейную и угловую скорости не только при равномерном движении точки по окружности, но- и при неравномерном движении тоже. Изменение модуля скорости точки за время Δt есть 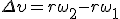, где ω2 и ω1 — угловые скорости в конце и в начале промежутка Δt. Разделим последнее равенство на Δt и учтем, что 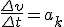и , тогда касательное ускорение

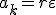. (3)

Соотношения (1), (2) и (3) дают для движущейся по окружности точки простую связь между линейными и угловыми величинами: линейная величина равна произведению радиуса окружности на соответствующую угловую величину. Эти соотношения получены нами для конкретной точки М колеса троллейбуса, но они справедливы и для любой другой точки вращающегося (как равномерно, так и неравномерно) тела.

Векторное произведение радиуса-вектора 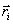материальной точки на ее импульс: 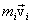называют моментом импульса 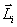, этой точки относительно точки О (рис.5.4)

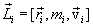. Вектор 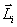иногда называют также моментом количества движения материальной точки. Он направлен вдоль оси вращения перпендикулярно плоскости, проведенной через векторы 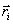и 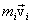и образует с ними правую тройку векторов (при наблюдении из вершины вектора видно, что вращение по кратчайшему расстоянию от 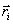к 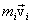происходит против часовой стрелки).

Векторную сумму моментов импульсов 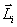всех материальных точек системы называют моментом импульса (количества движения) 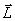системы относительно точки О:

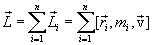
Векторы 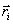и 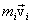взаимно перпендикулярны и лежат в плоскости перпендикулярной оси вращения тела. Поэтому . Сучетом связи линейных и угловых величин

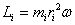
и направлен вдоль оси вращения тела в ту же сторону, что и вектор .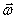

Таким образом.

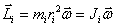
Момент импульса тела относительно оси вращения

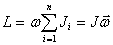
т.е.

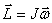
Следовательно, момент импульса тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость вращения тела вокруг этой оси.

.

.