-----------------------------------------------------------------------
1. Небольшой контур с током I помещен в неоднородное магнитное поле с индукцией 
. Плоскость контура перпендикулярна плоскости чертежа, но не перпендикулярна линиям индукции. Под действием поля контур …
| повернется против часовой стрелки и сместится влево |
| повернется против часовой стрелки и сместится вправо | |
| повернется по часовой стрелке и сместится вправо | |
| повернется по часовой стрелке и сместится влево |
-----------------------------------------------------------------------
Решение:
На контур с током в однородном магнитном поле действует вращающий момент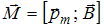 
, стремящийся расположить контур таким образом, чтобы вектор его магнитного момента 
был сонаправлен с вектором магнитной индукции поля. Если контур с током находится в неоднородном магнитном поле, то на него действует еще и результирующая сила, под действием которой незакрепленный контур втягивается в область более сильного поля, если угол между векторами и острый (α < 90°). Если же указанный угол тупой (α > 90°), то контур с током выталкивается в область более слабого поля, поворачивается под действием вращающего момента, так что угол становится острым, и затем втягивается в область более сильного поля. В соответствии с этим контурповернется против часовой стрелки и сместится влево.
-----------------------------------------------------------------------
2. Протон влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции и начинает двигаться по окружности. При увеличении кинетической энергии протона (если 
) в 4 раза радиус окружности …
|
| увеличится в 2 раза |
| увеличится в 4 раза | |
| уменьшится в 2 раза | |
| уменьшится в 4 раза |
-----------------------------------------------------------------------
Решение:
Радиус окружности, по которой движется заряженная частица в магнитном поле 
, где p – импульс частицы, связанный с ее кинетической энергией (при условии, что ) соотношением 
. Тогда 
, и при увеличении кинетической энергии протона в 4 раза радиус окружности увеличится в два раза.
-----------------------------------------------------------------------
3. На рисунке изображен вектор скорости движущегося электрона:
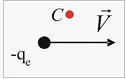
Вектор магнитной индукции 
поля, создаваемого электроном при движении, в точке С направлен …
|
| от нас |
| сверху вниз | |
| на нас | |
| снизу вверх |
-----------------------------------------------------------------------
Решение:
Индукция магнитного поля свободно движущегося заряда равна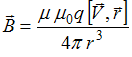 
, где 
заряд частицы, 
скорость частицы, 
радиус-вектор точки С. Используя определение векторного произведения, находим, что вектор 
направлен «на нас», но, учитывая отрицательный знак заряда частицы, получим окончательный ответ – вектор направлен «от нас».
-----------------------------------------------------------------------
4. Однозарядные ионы, имеющие одинаковые скорости, влетают в однородное магнитное поле. Их траектории приведены на рисунке:
Наименьшую массу имеет ион, движущийся по траектории …
|
| |
| характеристики траекторий не зависят от массы |
-----------------------------------------------------------------------
5. Два заряда 
и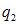 
движутся параллельно в одну сторону на расстоянии r друг от друга, как показано на рисунке:
Магнитная составляющая силы, действующей на второй заряд со стороны первого заряда, имеет направление …
|
| |
-----------------------------------------------------------------------
Решение:
Индукция магнитного поля свободно движущегося заряда равна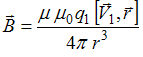 
, где 
заряд частицы, 
скорость частицы, радиус-вектор, характеризующий положение заряда 
относительно заряда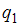 
. Используя определение векторного произведения, находим, что вектор в месте нахождения заряда направлен «от нас». Сила Лоренца 
по правилу левой руки имеет направление 4.
-----------------------------------------------------------------------
6. Электрон влетает в магнитное поле, создаваемое прямолинейным длинным проводником с током в направлении, параллельном проводнику (см. рис.).
При этом сила Лоренца, действующая на электрон, …
|
| лежит в плоскости чертежа и направлена влево |
| лежит в плоскости чертежа и направлена вправо | |
| перпендикулярна плоскости чертежа и направлена «от нас» | |
| перпендикулярна плоскости чертежа и направлена «к нам» |
-----------------------------------------------------------------------
Решение:
На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца. В данном случае магнитное поле создается прямолинейным длинным проводником с током I. В соответствии с правилом правого винта (буравчика) вектор магнитной индукции в месте расположения электрона направлен перпендикулярно плоскости чертежа «к нам». Поскольку скорость электрона перпендикулярна вектору магнитной индукции, для нахождения направления силы Лоренца удобно воспользоваться правилом левой руки. Учитывая знак заряда частицы, приходим к выводу, что сила Лоренца лежит в плоскости чертежа и направлена влево.
-----------------------------------------------------------------------
7. Поле создано прямолинейным длинным проводником с током I1. Если отрезок проводника с током I2 расположен в одной плоскости с длинным проводником так, как показано на рисунке, то сила Ампера …
|
| лежит в плоскости чертежа и направлена влево |
| лежит в плоскости чертежа и направлена вправо | |
| перпендикулярна плоскости чертежа и направлена «от нас» | |
| перпендикулярна плоскости чертежа и направлена «к нам» |
-----------------------------------------------------------------------
Решение:
На проводник с током в магнитном поле действует сила Ампера. В данном случае магнитное поле создается прямолинейным длинным проводником с током I1. В соответствии с правилом правого винта (буравчика) вектор магнитной индукции в месте расположения отрезка проводника с током I2 направлен перпендикулярно плоскости чертежа «от нас». В случае прямолинейного отрезка проводника с током в перпендикулярном проводнику магнитном поле для нахождения направления силы Ампера удобно воспользоваться правилом левой руки, согласно которому сила Ампера лежит в плоскости чертежа и направлена влево.
-----------------------------------------------------------------------
8. На рисунке изображены сечения двух параллельных прямолинейных длинных проводников с одинаково направленными токами, причем 
:
Индукция результирующего магнитного поля равна нулю в некоторой точке интервала …
|
| b |
| a | |
| c | |
| d |
-----------------------------------------------------------------------
Решение:
Линии магнитной индукции прямолинейных длинных проводников с токами 
и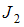 
представляют собой концентрические окружности, плоскости которых перпендикулярны проводникам, а центры лежат на их осях. Касательные к этим линиям в любой точке совпадают с направлением вектора магнитной индукции . Направления этих линий определяют правилом правого винта: направление вращения винта дает направление силовой линии магнитной индукции, если поступательное движение винта совпадает с направлением тока в проводнике. Индукция результирующего магнитного поля определяется по принципу суперпозиции 
и равна нулю, если векторы 
и 
противоположно направлены и равны по модулю. Это может быть только в точках интервалов b и c. Поскольку магнитная индукция прямолинейного длинного проводника с током вычисляется по формуле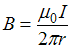 
, то модули векторов и равны, если 
, так как по условию . Следовательно, индукция результирующего магнитного поля равна нулю в некоторой точке интервала b.
-----------------------------------------------------------------------
9. На рисунке изображены сечения двух прямолинейных длинных параллельных проводников с противоположно направленными токами, причем 
. Индукция магнитного поля равна нулю на участке …
|
| d |
| а | |
| b | |
| c |
-----------------------------------------------------------------------
10. Рамка с током с магнитным дипольным моментом 
, направление которого указано на рисунке, находится в однородном магнитном поле:
Момент сил, действующих на магнитный диполь, направлен …
|
| перпендикулярно плоскости рисунка к нам |
| перпендикулярно плоскости рисунка от нас | |
| по направлению вектора магнитной индукции | |
| противоположно вектору магнитной индукции |
-----------------------------------------------------------------------
Решение:
Линии магнитной индукции прямолинейных длинных проводников с токами и 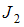представляют собой концентрические окружности, плоскости которых перпендикулярны проводникам, а центры лежат на их осях. Направления этих линий определяют правилом правого винта: направление вращения винта дает направление силовой линии магнитной индукции, если поступательное движение винта совпадает с направлением тока в проводнике. Индукция результирующего магнитного поля определяется по принципу суперпозиции и равна нулю, если векторы и противоположно направлены и равны по модулю. Это может быть только в точках интервалов а и d. Поскольку магнитная индукция прямолинейного длинного проводника с током вычисляется по формуле 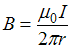, то модули векторов и равны, если 
, так как по условию . Следовательно, индукция результирующего магнитного поля равна нулю в некоторой точке интервала d.
-----------------------------------------------------------------------
Дата добавления: 2015-02-16; просмотров: 264 | Поможем написать вашу работу | Нарушение авторских прав |