Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Расчет траверсы на изгиб

Дано:

m– масса насоса,9800 кг = 9,8 т;

g – ускорение свободного падения, 9,81 м/ ;

R – расчетное сопротивление траверсы, 550 МПа;

k – коэффициент условий работы, 0,85.

1. Определяем нагрузку (P), действующую на траверсу, по формуле:

P=Gn =mgn ,

(3.1)

где G - вес поднимаемого груза;

m - масса поднимаемого груза;

g - ускорение свободного падения,g=9,81м/ ;

n - коэффициент перегрузки (n=1,1);

- коэффициент динамичности, ( = 1,1).

2. Рассчитываем максимальный изгибающий момент , возникающий в центральном сечении траверсы, по формуле

,

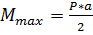(3.2)

где a - расстояние между точками подвеса груза, м.

3. Вычисляем требуемый момент сопротивления сечения траверсы по формуле

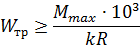
(3.3)

где k - коэффициент условий работы;

R - расчетное сопротивление материала траверсы, МПа.

;

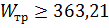
4.

5. По полученному значению требуемого момента сопротивления 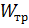выбрать профиль сечения с моментом сопротивления соблюдая при этом условие:

.

Выбираем двутавр №27 с моментом сопротивления .

Вывод: выполнила расчёт траверсы, работающие на изгиб, выбрала

двутавр №27 с моментом сопротивления .

Дано:

m – масса насоса, 8155 кг = 8,155 т;

α – угол, ;

φ˳ - коэффициент устойчивости стержня при продольном изгибе, 0,4;

R – расчетное сопротивление материала траверсы, 550 МПа;

µ - коэффициент приведения расчетной длины, 1;

g -ускорение свободного падения, 9,81 м/

1. Находим натяжение в каждой канатной подвеске, соединяющей траверсу с крюком грузоподъемного механизма, задавшись углом α= ;

(3.4)

N= ,

2. Подсчитываем разрывное усилие, взяв канатную подвеску в две нити и определяем по ГОСТ коэффициент запаса прочности, как грузового каната с легким режимом работы, - 5;

(3.5)

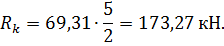
3. По найденному разрывному усилию, пользуясь таблицей ГОСТ 7668-80, подбираем стальной канат типа ЛК-РО конструкции 6 Х 36 (1 + 7 + 7/7 + + 14) + 1 с.с. для подвесок с характеристиками

4. Выбираем профиль сечения траверсы – из одного двутавра.

5. Определяем сжимающее усилие в траверсе:

(3.6)

где 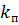- коэффициент перегрузки (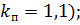

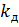- коэффициент динамичности (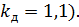

6. Находим требуемую площадь поперечного сечения траверсы, задаваясь коэффициентом продольного изгиба φ˳ - 0,4:

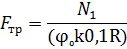
(3.7)

k – коэффициент условий работы траверсы, равный 0,85;

R - расчетное сопротивление материала траверсы, МПа.

7. По принятому профилю и выбираем двутавр № 12 с произвольным поперечным сечением

Определяем также радиус инерции сечения

8. Находим расчетную длину траверсы считая, что концы траверсы закреплены шарнирно:

(3.8)

где 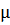- коэффициент приведения расчетной длины;

фактическая длина стержня траверсы,

9. Определяем гибкость траверсы:

(3.9)

=61,48

Причем необходимо, чтобы Здесь 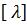максимально допустимая гибкость стержня траверсы для траверс из проката

Условие выполняется.

10. По найденному находим в таблице коэффициент продольного изгиба φ. При изменении от 0 до 2000 (φ) изменяется от 0,19 до 1.

φ=0,212.

11. Полученное сечение траверсы проверяем на устойчивость:

(3.10)

;

правильное сечение траверсы.

Вывод: выполнила расчёт траверсы сплошного сечения, работающей на сжатие, выбрала номер двутавра №10 по ГОСТ 8239-89 и условие траверсы на устойчивость выполнена