Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Уравновешивание вращающихся масс

7.3.1. Уравновешивание масс, находящихся в одной плоскости

Положения отдельных неуравновешенных масс , расположенных на роторе, можно охарактеризовать величинами радиус-векторов относительно оси его вращения. Система вращающихся масс будет уравновешена, если главный вектор сил инерции, действующих на эти массы при их совместном вращении, равен нулю:

,

где – сила инерции, действующая на i -ю массу; – сила инерции уравновешивающей массы , расположенной на расстоянии от оси вращения ротора.

Сила инерции, действующая на i -ю массу, вращающуюся с постоянной скоростью , равна .

Рассмотрим систему, состоящую из трех неуравновешенных вращающихся масс m₁, m₂ и m₃ (рис. 7.2).

а б

Рис. 7.2. Система неуравновешенных масс (а) и план сил инерции (б)

Условием уравновешенности данной системы масс является уравнение

.

Так как , то это уравнение можно записать в виде

.

Так как (мы рассматриваем вращающуюся систему масс), то

. (7.6)

Уравнение (7.6) можно решить аналитическим и графическим методами.

При аналитическом методе решения составляются уравнения проекций сил на координатные оси, из которых находят являющееся неизвестным последнее слагаемое.

Найдем и графическим методом, то есть построением векторного многоугольника (см. рис. 7.2б), являющегося графической интерпретацией векторного уравнения (7.6). Предварительно выбираем масштаб сил

,

где z₁ – длина вектора, изображающего силу , (мм).

Размерность масштаба (если масса задана в кг, радиус – в м).

Переведем масштабом другие известные слагаемые уравнения (7.6) в векторные отрезки:

Тогда векторное уравнение (7.6) запишется в виде

.

Построив векторный силовой многоугольник (см. рис. 7.2б) в масштабе , из него определим длину вектора . Выбрав из конструктивных соображений величину , вычисляем уравновеши-вающую массу

.

Поместив ее на роторе в направлении вектора на расстоянии от оси вращения, равном длине этого вектора, уравновесим ротор.

7.3.2. Уравновешивание вращающихся масс, расположенных произвольно

Последовательность уравновешивания масс, расположенных произ-вольно, рассмотрим на примере ротора с системой четырех неуравно-вешенных масс (рис. 7.3). Пусть известны величины неуравновешенных масс и их положения относительно оси вращения ротора, обусловленные радиусами – векторами и расстояниями относительно одной из произвольно выбранных плоскостей I, перпендикулярной оси вращения рассматриваемого ротора.

При вращении ротора и неуравновешенных масс с постоянной угловой скоростью на каждую из масс действует сила инерции

.

Так как угловая скорость в рассматриваемом здесь частном случае является величиной постоянной, то угловое ускорение отсутствует (ε = 0) и тангенциальная составляющая силы инерции равна нулю.

Рис. 7.3. Уравновешивание масс, расположенных произвольно:

а – вид на ротор с торца; б – вид на ротор с боку;

в – план сил при статическом уравновешивании;

г – план моментов сил при динамическом уравновешивании

Выбираем плоскости приведения I и II (см. рис. 7.3), в которых будем располагать уравновешивающие массы.

Задача заключается в том, что необходимо уравновесить массы динамически.

Сначала проводим статическое уравновешивание в плоскости I. Его последовательность описана в предыдущей главе.

, ,

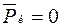. (7.7)

Используя (7.7), построим векторный многоугольник и графически найдем .

Уравновесим действие инерционных моментов, т.е. выполним условие . Для этого запишем уравнения

, . (7.8)

Так как , то из уравнения (7.8) следует, что

. (7.9)

Решая графически векторное уравнение (7.9), находим .

Предварительно выбираем масштаб

.

Тогда уравнение (7.9) запишется в виде

.

При этом принимаем, что векторы моментов повернуты на и совпадают с направлением .

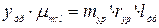. (7.10)

Находим из (7.10) величину , задавшись 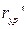, или наоборот. Здесь равна расстоянию между плоскостями приведения I и II.

Проводя от оси вращения ротора линию, параллельную , откладываем на ней с противоположных сторон и на концах этих векторов устанавливаем две уравновешивающие массы . Причем одна из них будет расположена в плоскости I, другая – в плоскости II. Массы и в плоскости I можно объединить в одну массу.