Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Кинематика работы колонны бурильных труб.

Здесь возможны два случая движения: 1) искривленная колонна вращается вокруг оси скважины как жесткое тело; 2) искривленная колонна вращается вокруг собственной оси как гибкий вал, т. е. такой вал, жесткость при изгибе которого равна нулю.

Закон распределения скоростей точек в поперечном сечении колонны для первого и второго случаев показан соответственно на рис. 1, а и 2, а (см. прил. 1).

Скорости точек M и M' в первом и втором случаях имеют соответственно значения:

(1)

где ω - угловая скорость вращателя; D - диаметр скважины; d - наружный диаметр трубы.

Пусть нагрузки, приложенные к колонне, таковы, что она искривляется и касается стенки скважины. Благодаря наличию сил сопротивления скорости в точках касания уменьшаются и становятся равными.

(2)

где k- коэффициент, характеризующий уменьшение скорости. Значения коэффициента kв двух приведенных выше формулах следовало бы взять различными. Примем в качестве приемлемого допущения, что они одинаковы.

Распределение скоростей в поперечном сечении колонны при некоторых значениях коэффициента k изображено на рис. 1, б и 2, б.

Величина введенного коэффициента kзависит от механических свойств породы, свойств промывочной жидкости, соотношений диаметров трубы и скважины и других факторов. Он может принимать значения в пределах от нуля до единицы. В частных случаях, при k = 0, колонна перекатывается по стенке скважины без скольжения, при k=1 стенки скважины не влияют на характер движения. Если колонна ведет себя как жесткое тело, то при k = 1 будет наблюдаться интенсивный односторонний износ труб.

При соприкосновении колонны со стенками скважины движение ее таково, что существует мгновенная ось вращения, проходящая через точку C_υ положение которой определяется в первом случае расстоянием M₁C_υ = kD/2 (рис. 1), а во втором M'₁C_υ=kd/2 (рис. 2).

Результирующие угловые скорости определяются в первом и втором случаях соответственно:

(3)

Скорость точки касания, согласно теореме сложения скоростей, будет равна:

(4)

Абсолютная, переносная и относительная скорости имеют значения:

Для первого случая:

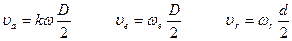(5)

Для второго случая:

(6)

Исходя из векторного уравнения (4) и учитывая соотношения (3) и (5), получаем для первого случая следующие величины переносной и относительной угловых скоростей:

(7)

где β = d/D.

Выполняя аналогичные преобразования, находим для второго случая:

(8)

Таким образом, бурильная колонна, перемещение которой ограничено стенками скважины, может вращаться одновременно вокруг оси скважины и вокруг собственной оси. Причем, если колонна ведет себя как жесткое тело, то она перекатывается по стенке скважины в сторону движения вращателя при k > β и в противоположную сторону при k < β. Если колонна ведет себя как гибкий вал, то она перекатывается по стенке скважины в сторону, противоположную движению вращателя.

Из формулы (7) можно увидеть, что при уменьшении радиальных зазоров, когда величина , угловая скорость вращения колонны вокруг оси скважины, направленная в сторону, противоположную движению вращателя, может значительно превосходить его угловую скорость. Это подтверждается экспериментально.[1] Представления о характере вращения колонны не только объясняются экспериментально установленными случаями сложного вращения колонны, но имеют и практическое приложение. При стендовых испытаниях можно найти угловые скорости вращения модели бурильной колонны труб вокруг собственной оси и оси вращателя установки. Тогда, пользуясь формулами (7) или (8), легко вычислить значение коэффициента k. Знание этого коэффициента позволяет прогнозировать характер вращения бурильных колонн в реальной скважине.