Читайте также:
|
Наиболее общая формулировка теоремы о равнораспределении гласит, что при определённых условиях (смотрите ниже), для физической системы с гамильтонианом H и степенями свободы xn, выполняется следующее соотношение для любых индексов m и n:
Здесь δmn — символ Кронекера, который равен единице если m=n и нулю в других случаях. Угловые скобки обозначают усреднение 
, которое может относиться как к усреднению по времени так и более общему усреднению по ансамблям в фазовом пространстве. Требования эргодичности используемое в теореме подразумевает, что эти два усреднения эквивалентны.
Общая формулировка теоремы верна как в случае микроканонического ансамбля, когда полная энергии системы постоянна, так и в случае канонического ансамбля, когда система связана с тепловым резервуаром, с которым она может обмениваться энергией. Вывод общей формулы приведён ниже.
Общая формула эквивалентна следующим выражениям:
1. 
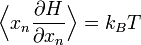для всех n.
2. 
для всех m≠n.
Если степень свободы xn появляется только в виде квадратичного слагаемого anxn² в гамильтониане H, то первая формула утверждает, что
в два раза больше вклада этой степени свободы в среднюю энергию 
. Тогда равнораспределение для системы с энергиями зависящими от квадратов координат следует из общей формулы. Аналогичный аргумент для степени s в общем случае применим для вклада вида anxns.
Степени свободы xn — координаты в фазовом пространстве системы и поэтому они обычно разделяют на обобщённые координаты qk и обобщённые импульсы pk, где pk — сопряжённый импульс к qk. В этом случае формула 1 означает, что для всех k
Используя уравнения гамильтоновой механики, эти формулы можно также переписать в виде
Формула 2 утверждает, что средние
и 
равны нулю для j≠k.
Дата добавления: 2015-01-30; просмотров: 111 | Поможем написать вашу работу | Нарушение авторских прав |