Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Прямая эластичность спроса по цене. Точечная, дуговая эластичность

Коэффициент прямой эластичности спроса по цене характеризует отношение относительного изменения объема спроса к относительному изменению цены и показывает, на сколько процентов изменяется объем спроса на товар при изменении его цены на 1%. Следовательно, его можно записать как

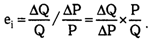(2.1)

Выделяют дуговую и точечную эластичность. Пусть дана какая-либо функция спроса:

Q₁= f(P₁),

где Q₁ – объем спроса на данный товар;

P₁– цена данного товара.

Изобразим эту функцию графически (рис. 2.5).

Рис.2.5. Определение дуговой эластичности

Предположим, что указанной функции спроса соответствует кривая, на которой произвольно взяты точки Е₁ и E₂. Причем точка Е₁ характеризуется ценой P₁ и объемом спроса Q₁, а точка E₂ – ценой Р₂ и объемом спросаQ₂. Очевидно, что при переходе от точки Е₁ к точке E₂ цена снижается с уровня P₁ до уровня P₂, а объем спроса возрастает от Q₁ до Q₂.

При расчете эластичности по вышеприведенной формуле неизбежно возникает следующий вопрос: если значения ΔQ и ΔР могут быть однозначно найдены и графически, и аналитически, поскольку определяются как ΔQ = Q₂ – Q₁; ΔР = Р₂ – Р_1, то какие значения Р и Q следует принять в качестве весов: базисные (Р₁ и Q₁) или новые (Р₂ и Q₂). Очевидно, что применение различных значений Р и Q приведет к разным результатам. Вследствие этого величины Р и Q для расчета коэффициента эластичности определяются чаще всего по правилу средних точек, то есть используются средние для данного интервала значения цены и спроса, а именно:

Формула (2.1) принимает в этом случае вид:

Таким образом, дуговая эластичность определяется как средняя эластичность.

Если функция спроса носит непрерывный характер, дуговая эластичность заменяется точечной, понимаемой как предел дуговой эластичности по мере того, как длина дуги стремится к нулю, то есть при бесконечно малом изменении цены.

В этом случае: