Читайте также:
|
Задача №6.
Решение:
Пусть мы имеем предикат P(x1, x2…, xn). Он может быть: тождественно ложным, тождественно ложным, выполнимым или опровержимым. Рассмотрим 2 случая по 2 варианта в каждом:
1) P(x1, x2…, xn) – тождественно истинный или опровержимый.
а) если P(x1, x2…, xn) – тождественно истинный, то λ[(
xi)(P(x1, x2…, xn))]=1, λ[( xj)(P(x1, x2…, xn))]=1=>
=>λ[( xj)( xi)(P(x1, x2…, xn))]=1, λ[( xj)( xi)(P(x1, x2…, xn))]=1 =>
=> ( xi)( xj)(P(x1, x2…, xn)) 1 ( xj)( xi)(P(x1, x2…, xn))
б)если P(x1, x2…, xn) – опровержимый, то λ[( xi)(P(x1, x2…, xn))]=0, λ[( xj)(P(x1, x2…, xn))]=0 =>
=>λ[( xj)( xi)(P(x1, x2…, xn))]=0, λ[( xj)( xi)(P(x1, x2…, xn))]=0 =>
=> ( xi)( xj)(P(x1, x2…, xn)) 1 ( xj)( xi)(P(x1, x2…, xn))
2) P(x1, x2…, xn) – тождественно ложный или выполнимый.
а) если P(x1, x2…, xn) – тождественно ложный, то λ[(
xi)(P(x1, x2…, xn))]=0, λ[(
xj)(P(x1, x2…, xn))]=0=>
=>λ[( xj)( xi)(P(x1, x2…, xn))]=0, λ[( xj)( xi)(P(x1, x2…, xn))]=0 =>
=> ( xi)( xj)(P(x1, x2…, xn)) 1 ( xj)( xi)(P(x1, x2…, xn))
б)если P(x1, x2…, xn) – выполнимый, то λ[( xi)(P(x1, x2…, xn))]=1, λ[( xj)(P(x1, x2…, xn))]=1 =>
=>λ[( xj)( xi)(P(x1, x2…, xn))]=1, λ[( xj)( xi)(P(x1, x2…, xn))]=1 =>
=> ( xi)( xj)(P(x1, x2…, xn)) 1 ( xj)( xi)(P(x1, x2…, xn))
Мы рассмотрели все возможные случаи и для каждого из них доказали, что если в формуле логики предикатов поменять местами два рядом стоящих одноименных квантора, то полученная формула будет равносильна исходной. А т.к. это справедливо для всех возможных случаев, правило можно обобщить на все случаи, т.е. на любой предикат и любые два одноимённых квантора:
( xi)( xj)(P(x1, x2…, xn)) 1 ( xj)( xi)(P(x1, x2…, xn))
( xi)( xj)(P(x1, x2…, xn)) 1 ( xj)( xi)(P(x1, x2…, xn))
(Хотя вообще-то это законы коммутативности)
Задача №7.
Постройте релейно-контактную схему с заданной функцией проводимости: x' (yz' vx(tyvz(xvy')))
Решение:
Как мы знаем, выражение типа x v y означает, что в схеме x и y соединены параллельно, а выражение типа xy означает, что x и y соединены последовательно. Исходя из этого по функции проводимости видно, что:
1) xиy' соединены параллельно
2) z и (xvy') соединены последовательно
3) t и y соединены последовательно
4) ty и z(xvy') соединены параллельно
5)x и tyvz(xvy') соединены последовательно
6)y и z' соединены последовательно
7)yz' и x(tyvz(xvy')) соединены параллельно
8)x' и yz' vx(tyvz(xvy')) соединены последовательно
Исходя из всего вышесказанного, построим контактно-релейную схему с заданной проводимостью:
| y |
| x |
| y’ |
| x’ |
| z’ |
| y |
| x |
| z |
| t |
Задача №8.
Доказать, что следующие функции примитивно рекурсивны:
a) f(x)=x+n;
б) f(х, у)=х+у;
в) f(х, у)=х! (здесь 0! = 1).
Функция примитивно рекурсивна, если она может быть получена из простейших функций: O(x)=0;S(x)=x+1; 
(x1,…,xn)=xm; с помощью конечного числа применений суперпозиции и примитивной рекурсии.
Функция, полученная суперпозицией примитивно рекурсивных функций, сама примитивно рекурсивна.
Решение:
а) f(x)=x+n;n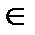 
(1,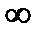 
);
x+1=S(x),
x+2=S(S(x)), обозначим S2(x),
x+3=S(S(S(x))), обозначим S3(x)
…
Тогда:
f(x) = x+n = S(S(…S(S(x))…)) = Sn(x), т.е.исходная функция получена с помощью n-кратной суперпозиции S(x). А функция, полученная суперпозицией примитивно рекурсивных функций, сама примитивно рекурсивна.
б) f(x,y)=x+y;
К ней можно применить операцию примитивной рекурсии, т.е функцию f(x,y), которая здесь двухместна, можно получить из одноместной F и трехместной G, где F и G – либо простейшие, либо примитивно рекурсивные, чтобы выполнялось:
f(x,y=0) = F(x);
f(x,y+1)=G(x,y,f(x,y));
Отсюда:
f(x,0)=x+0=x= 
(x);
f(x,y+1)=x+(y+1)=(x+y)+1=f(x,y)+1=S(f(x,y));
Т.е исходная функция может быть получена из и S; где и S – простейшие, следовательно – исходная функция примитивно рекурсивна.
в) f(x)=x! где 0!=1;
Данную функцию можно получить из простейших операцией примитивной рекурсии:
f(x=0) = F(0) (нульместная) = 0!=1=S(O(x)) – примитивно рекурсивна;
f(x+1) = G(x, f(x)) = x!(x+1) = f(x)*S(x);
Здесь функция G(u,v)=u*v, покажем, что она является примитивно рекурсивной, применив к ней операцию примитивной рекурсии:
G(u,v=0)=u*0=0=O(u);
G(u,v+1)=u*(v+1)=u*v+u=G(u,v)+ (u)=H(G, ) – примитивно рекурсивна (из предыдущего примера + суперпозиция), следовательно, G – примитивно рекурсивна,а следовательно и исходная функция также примитивно рекурсивна.
Задача №9.
Дата добавления: 2015-04-11; просмотров: 117 | Поможем написать вашу работу | Нарушение авторских прав |