Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Интерпретация параметров моделей с распределенным лагом

Рассмотрим модель с распределенным лагом в ее общем виде в предположении, что максимальная величина лага конечна: (3)

Эта модель говорит о том, что если в некоторый момент времени t происходит изменение независимой переменной х, то это изменение будет влиять на значения переменной у в течение t следующих моментов времени.

Коэффициент регрессии b₀ при переменной х_t характеризует среднее абсолютное изменение y _t при изменении х_t на 1 ед. своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором.

В момент (t + 1 ) совокупное воздействие факторной переменной х, на результату, составит (b₀ + b₁) усл. ед., в момент (t+2) это воздействие можно охарактеризовать суммой (b₀ + b₁ + b₂) и т. д. Полученные таким образом суммы называют промежуточными мультипликаторами.

С учетом конечной величины лага можно сказать, что изменение переменной х_t в момент t на 1 усл. ед. приведет к общему изменению результата через t моментов времени на (b₀ + b₁ +…+ b_l) абсолютных единиц.

Введем следующее обозначение: b₀ + b₁+...+ b_l = b. (4)

Величину b называют долгосрочным мультипликатором. Он показывает абсолютное изменение в долгосрочном периоде t + l результата у под влиянием изменения на 1 ед. фактора х.

Предположим (3.5)

Назовем полученные величины относительными коэффициентами модели с распределенным лагом. Если все коэффициенты b_j -имеют одинаковые знаки, то для любого. j

В этом случае относительные коэффициенты являются весами для соответствующих коэффициентов bj. Каждый из них измеряет долю общего изменения результативного признака в момент времени (t+j).

Зная величины , с помощью стандартных формул можно определить еще две важные характеристики модели множественной регрессии: величину среднего лага и медианного лага. Сред ний лаг определяется по формуле средней арифметической взвешенной: (6) и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени t. Небольшая величина среднего лага свидетельствует об относительно быстром реагировании результата на изменение фактора, тогда как высокое его значение говорит о том, что воздействие фактора на результат будет сказываться в течение длительного периода времени. Медианный лаг – это величина лага, для которого

Это тот период времени, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат.

Применение обычного МНК к таким моделям в большинстве случаев затруднительно по следующим причинам.

Во-первых, текущие и лаговые значения независимой переменной, как правило, тесно связаны друг с другом. Тем самым оценка параметров модели проводится в условиях высокой мультиколлинеарности факторов.

Во-вторых, при большой величине лага снижается число наблюдений, по которому строится модель, и увеличивается число ее факторных признаков. Это ведет к потере числа степеней свободы в модели.

В-третьих, в моделях с распределенным лагом часто возникает проблема автокорреляции остатков. Вышеуказанные обстоятельства приводят к значительной неопределенности относительно оценок параметров модели, снижению их точности и получению неэффективных оценок. Чистое влияние факторов на результат в таких условиях выявить невозможно. Поэтому на практике параметры моделей с распределенным лагом проводят в предположении определенных ограничений на коэффициенты регрессии и в условиях выбранной структуры лага.

Обратимся теперь к модели авторегрессии. Пусть имеется следующая модель: - (7)

Как и в модели с распределенным лагом, b₀ в этой модели характеризует краткосрочное изменение у_t под воздействием изменения х_t на 1 ед. Однако промежуточные и долгосрочный мультипликаторы в моделях авторегрессии несколько иные. К моменту времени (t + 1) результату, изменился под воздействием изменения изучаемого фактора в момент времени t на b₀ ед., а у_t+1 под воздействием своего изменения в непосредственно предшествующий момент времени - на c_t ед. Таким образом, общее абсолютное изменение результата в момент (t + 1) составит b₀ с₁ ед. Аналогично в момент времени (t +2) абсолютное изменение результата составит b₀ с₁² ед. и т. д. Следовательно, долгосрочный мультипликатор в модели авторегрессии можно рассчитать как сумму краткосрочного и промежуточных мультипликаторов: (8)

Учитывая, что практически во все модели авторегрессии вводится так называемое условие стабильности, состоящее в том, что коэффициент регрессии при переменной y_t по абсолютной вeличине меньше единицы |с₁| < 1, соотношение (8) можно преобразовать следующим образом:

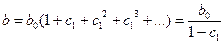(9)

Отметим, что такая интерпретация коэффициентов модели авторегрессии и расчет долгосрочного мультипликатора основаны на предпосылке о наличии бесконечного лага в воздействии текущего значения зависимой переменной на ее будущие значения.