
|
Читайте также: |
It is known that the area between the curve  and the lines
and the lines  ,
,  and
and  is given by
is given by
 .
.
If the equation of the curve is in parametric form
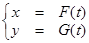 ,
,
where t is a parameter, and if

 is a continuous function on
is a continuous function on  , and
, and  does not change sign is in
does not change sign is in  , then the area of the region bounded by the curve
, then the area of the region bounded by the curve 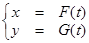 , the x-axis and the lines
, the x-axis and the lines  ,
,  is
is
 .
.
Example Find the area of the ellipse  , where
, where  ,
,  .
.
Computing Arc Lengths
Equations of curves are in Rectangular Form
Theorem If a curve  has a continuous derivative on
has a continuous derivative on  , then the length of the curve
, then the length of the curve  from
from  to
to  is given by
is given by
 .
.
If the equation of the curve is in the form  , then the length of the arc between
, then the length of the arc between 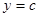 and
and 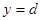 is given by
is given by
 .
.
Equations of Curves are in Parametric Form
Theorem When a function is expressed in parametric form  and
and  , the arc length
, the arc length  of the curve from
of the curve from 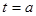 to
to  is given by
is given by
 .
.
Lecture 38 computing volumes and area of surfaces of revolution
Дата добавления: 2015-09-11; просмотров: 73 | Поможем написать вашу работу | Нарушение авторских прав |