Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Постановка

Струна довжиною L, лівий кінець мертво закріплений, правий на пружині k, на правому кінці мале тертя В (В<<1).

Знайти:

- затухання

- витікання мод

- коефіцієнт затухання τ (наближено)

2. Розв’язок

Умови однорідні, робимо розділення змінних:

Розв’язок для Х шукаємо у вигляді

Тому: (1)

Відповідно розв’язок для Т шукаємо у вигляді: (2)

Коли 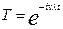=> (відповідну моду позначимо )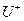

Підставляємо в праву межову умову:

В<<1, b<<1

Робимо послідовні наближення:

Це – трансцендентне рівняння, його розв’язки знаходимо графічним способом:

будуємо графіки f=y/a (зелений графік), f= - tan(y) (червоний графік):

Іксові координати точок перетину графіків і будуть шуканими розв’язками.

Нульовий розв’язок існує завжди. Розв’язків буде безліч, якщо а скінченне.

Коли то розв’язки прямують до , тобто нулі похідної від синуса, що відповідає вільному кінцю (нескінченно м’яка пружина). Коли - розв’язки прямують до , тобто нулі синуса, що відповідає закріпленому кінцю (нескінченно жорстка пружина).

У нульовому наближенні по В це є розв’язки задачі з правою межовою умовою 3-го роду.

Звідси маємо набір у нульовому наближенні.

Рахуємо перше наближення:

(3)

!!! Так як другий доданок має бути малим, то таке наближення годиться лише для не

надто великих (тобто обмеженої кількості) λ.

Маємо:

(4)

(5)

У виразі (3) є спадна з часом експонента => затухання, при чому коефіцієнт затухання для j-ої моди (6)

Із (4) маємо:

Так як мале то , ,

Тобто маємо в нульовому наближенні звичний вираз

Коли 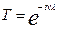=> (відповідну моду позначимо )

Роблячи аналогічні викладки отримаємо:

(4`)

(5)

Витікаючі моди:

Розпишемо повністю одну моду:

Маємо дві хвилі різних напрямків поширень. Коли β =0 то маємо звичайні хвилі,

тут:

- затухання з часом

- право біжуча хвиля наростає з ліва на право

- ліво біжуча хвиля наростає з права на ліво

- при х =0 (лівий край) маємо умову зшиваня (рівні амплітуди), звідси бачимо, що потік енергії через правий край відмінний від нуля і направлений назовні