
Читайте также:
|
Раздел 4. Расчет числа соединительных устройств и каналов в коммутационных системах с отказами.
Обслуживание вызовов симметричного потока с простым последействием
Постановка задачи. Исходными данными модели являются: неблокирующая коммутационная система (никаких других ограничений на структуру системы не накладывается – она может быть однозвеньевой или многозвеньевой);
в выходы коммутационной системы включен полнодоступный пучок емкостью 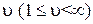 линий (приборов);
линий (приборов);
вызовы, поступающие на входы коммутационной системы, образуют симметричный поток с простым последействием с параметром  ;
;
дисциплина обслуживания коммутационной системой поступающего потока вызовов – с потерями;
длительность обслуживания Т коммутационной системой вызова является случайной величиной, распределенной по показательному закону, то есть функция распределения длительности занятия
 ,
,
где 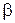 – параметр длительности занятия. Обычно за единицу времени принимается средняя длительность занятия –
– параметр длительности занятия. Обычно за единицу времени принимается средняя длительность занятия –  , следовательно, и
, следовательно, и 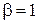 .
.
Задача формулируется следующим образом. Полнодоступный пучок емкостью  линий, включенных в выходы неблокирующей коммутационной системы с потерями, обслуживает вызовы, образующие симметричный поток с простым последействием с параметром
линий, включенных в выходы неблокирующей коммутационной системы с потерями, обслуживает вызовы, образующие симметричный поток с простым последействием с параметром  . Длительность обслуживания вызова коммутационной системой распределена по показательному закону. Требуется определить вероятности различных состояний полнодоступного пучка в процессе обслуживания поступающих вызовов.
. Длительность обслуживания вызова коммутационной системой распределена по показательному закону. Требуется определить вероятности различных состояний полнодоступного пучка в процессе обслуживания поступающих вызовов.
В этой задаче достаточно исследовать макросостояния системы, то есть состояния, различающиеся числом i одновременно занятых линий в любой момент времени (i = 0, 1, 2,...,  ), независимо от того, какие именно линии заняты. Это объясняется следующими соображениями.
), независимо от того, какие именно линии заняты. Это объясняется следующими соображениями.
1. При любом состоянии полнодоступного пучка линий, включенных в выходы неблокирующей коммутационной системы, т. е. при любом числе занятых линий, независимо от того, какие именно линии заняты, любой поступивший вызов может быть обслужен любой из свободных в данный момент линий пучка. Поступивший вызов получает отказ в обслуживании (теряется) только в тех случаях, когда в момент поступления вызова все  линий пучка заняты. Указанное свойство полнодоступного пучка не зависит ни от структуры полнодоступного пучка (прямое или сдвинутое включение линий пучка в объединяемые выходы коммутационной системы), ни от способа искания свободной линии пучка (с исходного положения, в случайном или любом другом порядке).
линий пучка заняты. Указанное свойство полнодоступного пучка не зависит ни от структуры полнодоступного пучка (прямое или сдвинутое включение линий пучка в объединяемые выходы коммутационной системы), ни от способа искания свободной линии пучка (с исходного положения, в случайном или любом другом порядке).
2. Пучок линий обслуживает вызовы симметричного потока, параметр которого  , зависит в любой момент времени только от состояния данного пучка. Параметр
, зависит в любой момент времени только от состояния данного пучка. Параметр  задается какой-либо зависимостью лишь от числа занятых (или от числа свободных) линий и не зависит от того, какие именно линии пучка заняты.
задается какой-либо зависимостью лишь от числа занятых (или от числа свободных) линий и не зависит от того, какие именно линии пучка заняты.
Из этих соображений следует, что вероятности занятости фиксированного числа линий не зависят от того, какие именно линии заняты, а зависят только от числа занятых линий. Определим вероятности различных макросостояний системы – вероятности того, что в системе в момент времени t занято точно i линий пучка (i =0, 1, 2,...,  ) –
) –  . Помимо того, определим вероятности потерь по времени
. Помимо того, определим вероятности потерь по времени  и по вызовам
и по вызовам  .
.
Число занятых линий i в момент t является случайным. Поэтому процесс изменения числа занятых линий во времени является случайным процессом. Если известно, что в момент t занято i линий, то последующее течение процесса изменения числа занятых линий в вероятностном смысле зависит только от моментов появления новых вызовов и от моментов окончания занятий линий как вызовами, поступившими до момента t, так и новыми вызовами.
Моменты появления новых вызовов не зависят от рассматриваемого случайного процесса до момента t, так как параметр  поступающего на систему симметричного потока вызовов зависит только от числа i занятых линий в рассматриваемый момент t. Также от течения процесса до момента t не зависят и моменты окончания занятий линий. Последнее следует из показательного распределения длительности занятий, при котором время оставшейся части занятия не зависит от того, сколько времени оно уже продолжается (основное свойство показательного распределения).
поступающего на систему симметричного потока вызовов зависит только от числа i занятых линий в рассматриваемый момент t. Также от течения процесса до момента t не зависят и моменты окончания занятий линий. Последнее следует из показательного распределения длительности занятий, при котором время оставшейся части занятия не зависит от того, сколько времени оно уже продолжается (основное свойство показательного распределения).
Отсюда рассматриваемый случайный процесс обладает следующим свойством: если известно число занятых линий в момент времени t, то процесс изменения состояний системы после момента t в вероятностном смысле не зависит от течения процесса до этого момента, т. е. рассматриваемый процесс является марковским.
Понятие о марковских процессах. Для марковских процессов, названных в честь выдающегося русского математика А. А. Маркова (1856 – 1922 гг.), будущее определяется известным настоящим и не зависит от прошлого.
Пусть V(t) – число занятых линий в момент времени t. Если в некоторый момент t в системе занято i линий (система находится в состоянии i), то V (t) =i, i = 0, 1, 2,..., u. Система имеет конечное число (u+1) состояний, и рассматриваемый марковский процесс является процессом с конечным числом состояний. Обозначим через  вероятность того, что система, находившаяся в момент
вероятность того, что система, находившаяся в момент 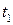 в состоянии j, за время
в состоянии j, за время  перейдет в состояние i. Рассматриваемый случайный процесс, т. е. процесс поступления вызовов и освобождений, зависит лишь от числа занятых линий j в начальный момент
перейдет в состояние i. Рассматриваемый случайный процесс, т. е. процесс поступления вызовов и освобождений, зависит лишь от числа занятых линий j в начальный момент 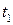 и от длины отрезка времени
и от длины отрезка времени  . Этот процесс не зависит от моментов
. Этот процесс не зависит от моментов 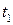 и
и  . Поэтому и вероятность
. Поэтому и вероятность  зависит только от длины отрезка времени
зависит только от длины отрезка времени  и значений j и i. Процессы Маркова, обладающие таким свойством, называются однородными.
и значений j и i. Процессы Маркова, обладающие таким свойством, называются однородными.
Выделим на отрезке времени  момент
момент  . Для того чтобы за промежуток времени
. Для того чтобы за промежуток времени  система перешла из состояния j, в котором она находилась в момент
система перешла из состояния j, в котором она находилась в момент 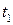 , в состояние i в момент
, в состояние i в момент  , система должна за отрезок времени
, система должна за отрезок времени  перейти в некоторое состояние
перейти в некоторое состояние  , а потом за оставшийся отрезок времени
, а потом за оставшийся отрезок времени 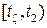 – из состояния r в состояние i. По формуле полной вероятности получаем
– из состояния r в состояние i. По формуле полной вероятности получаем
 (4.1)
(4.1)
Формула (4.1) называется уравнением Колмогорова–Чепмена. В силу свойства процесса Маркова вероятность  является безусловной, не зависящей от процесса, протекающего на отрезке времени
является безусловной, не зависящей от процесса, протекающего на отрезке времени 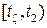 , так как известно, что в момент
, так как известно, что в момент  система находится в состоянии
система находится в состоянии  .
.
В формуле (4.1) изменим обозначения отрезков времени:  обозначим через
обозначим через 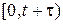 , тогда
, тогда 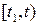 будет
будет  и
и  . При этом (4.1) преобразуется к виду
. При этом (4.1) преобразуется к виду
 (4.2)
(4.2)
Для решения задачи обслуживания полнодоступным пучком вызовов симметричного потока удобно воспользоваться частным случаем процесса Маркова – процессом рождения и гибели.
Процесс рождения и гибели – это марковский процесс с непрерывным параметром t, имеющий конечное (0, 1, 2,..., i,.., u) или счетное (0, 1, 2,.., i,...) множество состояний, в каждом из которых за бесконечно малый промежуток времени  с вероятностью более нуля возможен непосредственный переход системы только в соседнее состояние, иными словами, из состояния i возможен либо непосредственный переход в состояние
с вероятностью более нуля возможен непосредственный переход системы только в соседнее состояние, иными словами, из состояния i возможен либо непосредственный переход в состояние 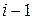 или
или  , либо система остается в состоянии i. При этом вероятность того, что за время
, либо система остается в состоянии i. При этом вероятность того, что за время 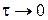 произойдет более одного изменения состояния, равна
произойдет более одного изменения состояния, равна  .
.
Определение вероятностей состояния полнодоступного пучка. Не ограничивая пока емкости пучка линий  , определим вероятности
, определим вероятности  того, что в момент
того, что в момент  пучок находится в состоянии i.
пучок находится в состоянии i.
Так как симметричный поток является ординарным и параметр его в момент t не зависит от процесса обслуживания вызовов до момента t, то процесс обслуживания вызовов данного потока полнодоступным пучком линий представляет собой процесс рождения и гибели. Диаграмма состояний и переходов этого процесса приведена на рис. 4.1.

Рисунок 4.1 – Диаграмма переходов в марковской цепи
Процесс рождения в рассматриваемой задаче отождествляется с процессом занятий, а процесс гибели – с процессом освобождений линий пучка. Параметры потоков занятий и освобождений обозначены соответственно  , и
, и  , i =0, 1, 2,... Согласно процессу рождения и гибели, при
, i =0, 1, 2,... Согласно процессу рождения и гибели, при 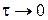 пучок в момент
пучок в момент  может находиться в состоянии i только при наличии следующих условий.
может находиться в состоянии i только при наличии следующих условий.
1. В момент t пучок находится в состоянии 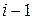 (вероятность этого события
(вероятность этого события  ), и за время t на обслуживание поступит точно один вызов (вероятность данного события
), и за время t на обслуживание поступит точно один вызов (вероятность данного события  ). Тогда вероятность перехода пучка за промежуток времени
). Тогда вероятность перехода пучка за промежуток времени  из состояния
из состояния 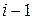 в состояние i составляет
в состояние i составляет  . При этом вероятность
. При этом вероятность  является условной. Она определяется с учетом того, что в момент t пучок находился в состоянии
является условной. Она определяется с учетом того, что в момент t пучок находился в состоянии 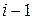 .
.
2. В момент t пучок находится в состоянии  (вероятность этого события
(вероятность этого события  ), и за время t освободится точно одна из
), и за время t освободится точно одна из  занятых линий (вероятность этого события
занятых линий (вероятность этого события 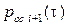 ). Вероятность перехода пучка за промежуток времени
). Вероятность перехода пучка за промежуток времени  из состояния
из состояния  в состояние i составляет
в состояние i составляет 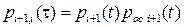 . Вероятность
. Вероятность 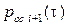 является условной, она определяется с учетом того, что в момент t пучок находился в состоянии
является условной, она определяется с учетом того, что в момент t пучок находился в состоянии  .
.
3. В момент t пучок находится в состоянии i (вероятность этого события  ). За время t пучок не изменяет своего состояния, он остается в состоянии i, т. е. на пучок не поступает вызова и в нем не освобождается ни одна из занятых линий [вероятность этого события
). За время t пучок не изменяет своего состояния, он остается в состоянии i, т. е. на пучок не поступает вызова и в нем не освобождается ни одна из занятых линий [вероятность этого события  ]. Вероятность перехода пучка из состояния i в состояние i составляет
]. Вероятность перехода пучка из состояния i в состояние i составляет  .
.
4. За время  в пучке происходят два и более переходов в результате поступления двух и более вызовов, либо освобождения двух и более линий, либо поступления одного и более вызовов и одновременно освобождения одной и более линий. Вероятность таких событий составляет
в пучке происходят два и более переходов в результате поступления двух и более вызовов, либо освобождения двух и более линий, либо поступления одного и более вызовов и одновременно освобождения одной и более линий. Вероятность таких событий составляет  .
.
Условия 1 – 4 взаимно исключают друг друга, поэтому искомые вероятности  , (i =0, 1, 2,...), определяются как сумма приведенных выше четырех вероятностей:
, (i =0, 1, 2,...), определяются как сумма приведенных выше четырех вероятностей:
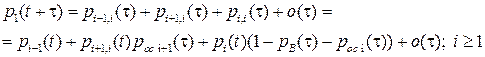 (4.3)
(4.3)
Найдем вероятность поступления точно одного вызова  за отрезок времени
за отрезок времени  и вероятность освобождения точно одной из
и вероятность освобождения точно одной из  занятых линий за тот же отрезок времени –
занятых линий за тот же отрезок времени –  .
.
Вероятность  . Из определения параметра потока в произвольный момент
. Из определения параметра потока в произвольный момент  (см. главу 2)
(см. главу 2)  следует, что вероятность поступления одного и более вызовов за отрезок времени
следует, что вероятность поступления одного и более вызовов за отрезок времени  составляет
составляет  . Для симметричного потока параметр которого
. Для симметричного потока параметр которого  зависит только от числа занятых в момент
зависит только от числа занятых в момент  линий,
линий,  . Так как симметричный поток является ординарным, то вероятность поступления двух и более вызовов за бесконечно малый отрезок времени
. Так как симметричный поток является ординарным, то вероятность поступления двух и более вызовов за бесконечно малый отрезок времени  составляет
составляет  . Отсюда
. Отсюда  . Учитывая, что
. Учитывая, что  и
и  – бесконечно малые одного порядка, получим
– бесконечно малые одного порядка, получим
 (4.4)
(4.4)
Вероятность  . Вероятность освобождения за время
. Вероятность освобождения за время 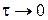 одной из r занятых линий не зависит от характера поступающего потока вызовов. Вероятность
одной из r занятых линий не зависит от характера поступающего потока вызовов. Вероятность  зависит только от состояния r пучка в момент t и от закона распределения длительности обслуживания, который задан показательным. Вероятность освобождения хотя бы одной из r занятых линий за промежуток времени t в соответствии с (2.45) равна
зависит только от состояния r пучка в момент t и от закона распределения длительности обслуживания, который задан показательным. Вероятность освобождения хотя бы одной из r занятых линий за промежуток времени t в соответствии с (2.45) равна
 (4.5)
(4.5)
Так как в рассматриваемой задаче за единицу времени принята средняя длительность занятия, то 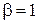 . Поток освобождений является ординарным. Отсюда вероятность освобождения точно одной из r занятых линий за отрезок времени
. Поток освобождений является ординарным. Отсюда вероятность освобождения точно одной из r занятых линий за отрезок времени  при
при 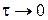 равна
равна
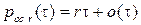 (4.6)
(4.6)
Заметим, что вероятности  , определяемые (4.1), так же как и вероятности
, определяемые (4.1), так же как и вероятности  , определяемые (4.6), пропорциональны t. Следовательно, вероятности поступления за время t любых двух и более событий (двух и более вызовов, или двух и более освобождений, или вызова и освобождения и т. д.) есть величины порядка
, определяемые (4.6), пропорциональны t. Следовательно, вероятности поступления за время t любых двух и более событий (двух и более вызовов, или двух и более освобождений, или вызова и освобождения и т. д.) есть величины порядка  . Из этого следует, что вероятности
. Из этого следует, что вероятности  перехода системы за отрезок времени
перехода системы за отрезок времени  из состояния r в состояние i при
из состояния r в состояние i при  равны
равны 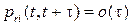 ,
,  .
.
Подставим в систему уравнений (4.3) полученные значения вероятностей  и
и 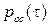 , перенесем из правой части уравнений в левую
, перенесем из правой части уравнений в левую  , просуммируем все бесконечно малые слагаемые
, просуммируем все бесконечно малые слагаемые  и разделим обе части уравнений на t. В результате получим
и разделим обе части уравнений на t. В результате получим
 ,
, 
Переходя к пределу 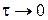 , найдем
, найдем
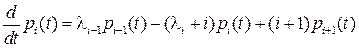 ,
, 
При  переход системы из состояния
переход системы из состояния 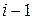 в состояние
в состояние  не имеет места. Поэтому
не имеет места. Поэтому

Получаем для определения вероятностей  , (i =0, 1, 2,…..), систему дифференциальных уравнений
, (i =0, 1, 2,…..), систему дифференциальных уравнений
 (4.7)
(4.7)
Допускаем, что при 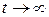 для вероятностей
для вероятностей  существуют конечные пределы (стационарные вероятности) –
существуют конечные пределы (стационарные вероятности) – 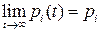 . Тогда
. Тогда 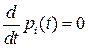 . Полагая в системе уравнений (4.7)
. Полагая в системе уравнений (4.7) 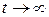 , получаем систему линейных алгебраических уравнений
, получаем систему линейных алгебраических уравнений
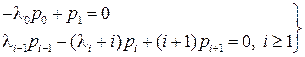 (4.8)
(4.8)
Обозначим в (4.8)  , получим
, получим  ;
;  .
.
Отсюда  , и, следовательно
, и, следовательно
 (4.9)
(4.9)
Выражая вероятность  через
через  , получим
, получим 
 (4.10)
(4.10)
В (4.10) принято обозначение  . Если ряд
. Если ряд  расходится, то вызовы поступают настолько чаще по сравнению с освобождениями занятых линий, что, начиная с некоторого момента времени, окажется невозможным обслуживание коммутационной системой поступающего потока вызовов. Для сходимости ряда необходимо, чтобы параметр потока вызовов
расходится, то вызовы поступают настолько чаще по сравнению с освобождениями занятых линий, что, начиная с некоторого момента времени, окажется невозможным обслуживание коммутационной системой поступающего потока вызовов. Для сходимости ряда необходимо, чтобы параметр потока вызовов  существенно не отличался от параметра потока освобождений. Это условие выполняется в рассматриваемой задаче обслуживания полнодоступным пучком линий симметричного потока вызовов. Доказано, что при любом t (доказательство не приводится), если ряд сходится, то
существенно не отличался от параметра потока освобождений. Это условие выполняется в рассматриваемой задаче обслуживания полнодоступным пучком линий симметричного потока вызовов. Доказано, что при любом t (доказательство не приводится), если ряд сходится, то  . Исходя из этого, при
. Исходя из этого, при 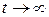 , используя «нормировочное» условие
, используя «нормировочное» условие  , из (4.10) и (4.9) получим:
, из (4.10) и (4.9) получим:
 (4.11)
(4.11)
В общем случае для процесса рождения и гибели со счетным множеством состояний с параметрами  , и
, и  , i =0, 1, 2,..., стационарные вероятности состояний определяются следующими выражениями:
, i =0, 1, 2,..., стационарные вероятности состояний определяются следующими выражениями:
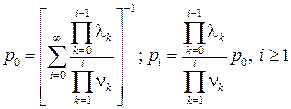 (4.12)
(4.12)
В рассматриваемой задаче обслуживания полнодоступным пучком емкостью  линий симметричного потока вызовов параметр потока вызовов
линий симметричного потока вызовов параметр потока вызовов  и параметр потока освобождений
и параметр потока освобождений  конечны; число состояний также является величиной конечной, оно равно
конечны; число состояний также является величиной конечной, оно равно  , так что
, так что 
При этом если система находится в состоянии  (все линии заняты), то поступающие вызовы не могут производить новых занятий и, следовательно, для
(все линии заняты), то поступающие вызовы не могут производить новых занятий и, следовательно, для  параметр потока занятий
параметр потока занятий  . В состоянии
. В состоянии  все линии свободны и параметр потока освобождений
все линии свободны и параметр потока освобождений 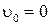 . С учетом этого вероятности
. С учетом этого вероятности  и
и  определяются формулами
определяются формулами
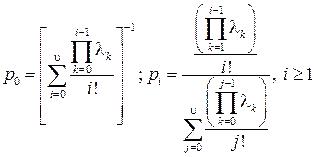 (4.13)
(4.13)
Определение вероятностей потерь по времени и потерь по вызовам. Вероятность  можно рассматривать как долю времени (на промежутке
можно рассматривать как долю времени (на промежутке  ), в течение которого в пучке занято точно i линий. В частности, доля времени (на промежутке
), в течение которого в пучке занято точно i линий. В частности, доля времени (на промежутке  ), в течение которого заняты все
), в течение которого заняты все  линий полнодоступного пучка, равна вероятности
линий полнодоступного пучка, равна вероятности  . Применительно к полнодоступному пучку линий, включенных в выходы неблокирующей коммутационной системы, вероятность потерь по времени
. Применительно к полнодоступному пучку линий, включенных в выходы неблокирующей коммутационной системы, вероятность потерь по времени  представляет собой долю времени (на промежутке
представляет собой долю времени (на промежутке  ), в течение которого заняты все
), в течение которого заняты все  линий пучка, и определяется соотношением
линий пучка, и определяется соотношением
 (4.14)
(4.14)
Определим вероятность потерь по вызовам  . Согласно определению
. Согласно определению  есть отношение интенсивности потерянного
есть отношение интенсивности потерянного  к интенсивности поступающего
к интенсивности поступающего 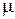 потоков вызовов:
потоков вызовов: 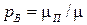 . Здесь
. Здесь
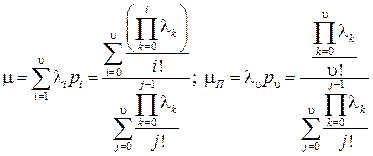 ;
;
Следовательно,
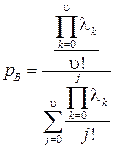 (4.15)
(4.15)
(в целях идентичности с формулами  и
и  в (4.15) индекс суммирования i заменен на j).
в (4.15) индекс суммирования i заменен на j).
4.2. Обслуживание вызовов простейшего потока
Полнодоступный пучок емкостью  линий, который включен в неблокирующую коммутационную систему с потерями, обслуживает вызовы, образующие простейший поток с параметром
линий, который включен в неблокирующую коммутационную систему с потерями, обслуживает вызовы, образующие простейший поток с параметром  . Длительность обслуживания вызова коммутационной системой распределена по показательному закону
. Длительность обслуживания вызова коммутационной системой распределена по показательному закону  . Требуется определить вероятности различных состояний полнодоступного пучка в процессе обслуживания поступающих вызовов и вероятности потерь по времени
. Требуется определить вероятности различных состояний полнодоступного пучка в процессе обслуживания поступающих вызовов и вероятности потерь по времени  , по вызовам
, по вызовам  и по нагрузке
и по нагрузке  .
.
Параметр простейшего потока  является постоянной величиной, не зависящей от состояния коммутационной системы. Поэтому в (4.13) – (4.15) при любых значениях k вместо
является постоянной величиной, не зависящей от состояния коммутационной системы. Поэтому в (4.13) – (4.15) при любых значениях k вместо  используется величина
используется величина  , и эти формулы преобразуются к виду:
, и эти формулы преобразуются к виду:
 (4.16)
(4.16)
 (4.17)
(4.17)
Сокращая числитель и знаменатель на  , получим
, получим
 (4.18)
(4.18)
Формула (4.16) называется распределением Эрланга. Она показывает, что вероятность  зависит только от числа занятых линий i, емкости пучка
зависит только от числа занятых линий i, емкости пучка  и величины параметра потока вызовов
и величины параметра потока вызовов  . По этим соображениям вероятность
. По этим соображениям вероятность  принято обозначать
принято обозначать  , а вероятность
, а вероятность  – через
– через  или
или 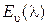 .
.
Из (4.17) и (4.18) следует, что
 (4.19)
(4.19)
При выводе (4.13) – (4.15), а следовательно, и (4.16) – (4.18) средняя длительность занятия принята равной единице; отсюда и параметр длительности занятий при показательном законе распределения 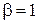 . В общем случае при измерении длительности занятий в любых единицах времени
. В общем случае при измерении длительности занятий в любых единицах времени  распределение Эрланга имеет следующий вид:
распределение Эрланга имеет следующий вид:
 (4.20)
(4.20)
Установим зависимость вероятностей  от интенсивности поступающей нагрузки у:
от интенсивности поступающей нагрузки у:  `
`  , где
, где 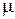 – интенсивность потока вызовов;
– интенсивность потока вызовов;  – средняя длительность занятия. Для простейшего потока, который является ординарным и стационарным,
– средняя длительность занятия. Для простейшего потока, который является ординарным и стационарным, 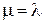 . Тогда распределение Эрланга имеет вид:
. Тогда распределение Эрланга имеет вид:
 (4.21)
(4.21)

и, в частности, вероятность того, что в полнодоступном пучке заняты все  линий (
линий ( ), равна
), равна
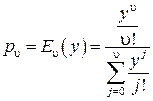 (4.22)
(4.22)
При 
 распределение Эрланга (4.21) преобразуется в распределение Пуассона:
распределение Эрланга (4.21) преобразуется в распределение Пуассона:
 (4.23)
(4.23)
В (4.23)  есть вероятность того, что в произвольный момент t бесконечный пучок находится в состоянии i.
есть вероятность того, что в произвольный момент t бесконечный пучок находится в состоянии i.
Распределение Эрланга определено в предположении показательного распределения длительности занятий. Б. А. Севастьянов показал, что полученная формула справедлива при произвольном (а не только показательном) распределении длительности занятий, если средняя длительность занятий является конечной величиной.
Логический анализ вероятностей  .
.
1. Вероятность  – вероятность того, что в произвольный момент времени t стационарного режима в полнодоступном пучке емкостью
– вероятность того, что в произвольный момент времени t стационарного режима в полнодоступном пучке емкостью  линий, который работает в режиме с потерями и обслуживает поступающую нагрузку интенсивностью у, создаваемую простейшим потоком вызовов, занято точно i линий.
линий, который работает в режиме с потерями и обслуживает поступающую нагрузку интенсивностью у, создаваемую простейшим потоком вызовов, занято точно i линий.
2. Пусть имеется  полнодоступных пучков одной и той же емкости
полнодоступных пучков одной и той же емкости  , на каждый из которых поступает нагрузка интенсивностью у. Тогда вероятность
, на каждый из которых поступает нагрузка интенсивностью у. Тогда вероятность  – доля пучков, в которых в произвольный момент t занято точно по i линий, т. е.
– доля пучков, в которых в произвольный момент t занято точно по i линий, т. е.
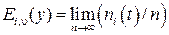
где  –число пучков, которые в момент t находятся в состоянии i.
–число пучков, которые в момент t находятся в состоянии i.
3. Если фиксировать состояния определенного полнодоступного пучка в  произвольных моментов времени t, то
произвольных моментов времени t, то  есть доля моментов t, в которые пучок находится в состоянии i, т. е.
есть доля моментов t, в которые пучок находится в состоянии i, т. е.
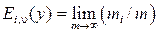
где  – число произвольных моментов t, в которые в пучке занято точно i линий.
– число произвольных моментов t, в которые в пучке занято точно i линий.
4. Вероятность  –доля времени (на промежутке
–доля времени (на промежутке  ), в течение которого в полнодоступном пучке занято точно i линий (пучок емкостью
), в течение которого в полнодоступном пучке занято точно i линий (пучок емкостью  линий обслуживает поступающую нагрузку у). В частности, доля времени (на промежутке
линий обслуживает поступающую нагрузку у). В частности, доля времени (на промежутке  ), в течение которого заняты все u линий полнодоступного пучка, равна вероятности
), в течение которого заняты все u линий полнодоступного пучка, равна вероятности  , определяемой по (4.22).
, определяемой по (4.22).
Вероятность потерь по нагрузке. Математическое ожидание и дисперсия нагрузки. Вероятность потерь по нагрузке  найдем из соотношения
найдем из соотношения
 , (4.24)
, (4.24)
где  – интенсивность потерянной
– интенсивность потерянной  – интенсивность поступающей нагрузок. Учитывая, что
– интенсивность поступающей нагрузок. Учитывая, что  , определим интенсивность обслуженной полнодосупным пучком нагрузки
, определим интенсивность обслуженной полнодосупным пучком нагрузки  , которая равна математическому ожиданию нагрузки, обслуженной в единицу времени. По теореме о количественной оценке обслуженной нагрузки
, которая равна математическому ожиданию нагрузки, обслуженной в единицу времени. По теореме о количественной оценке обслуженной нагрузки
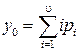 , (4.25)
, (4.25)
где i – число занятых линий в пучке;  – вероятность нахождения пучка в произвольный момент времени в состоянии i. Правая часть выражения (4.25) соответствует математическому ожиданию числа одновременно занятых линий, т. е. интенсивность обслуженной нагрузки равна математическому ожиданию числа одновременно занятых линий пучка.
– вероятность нахождения пучка в произвольный момент времени в состоянии i. Правая часть выражения (4.25) соответствует математическому ожиданию числа одновременно занятых линий, т. е. интенсивность обслуженной нагрузки равна математическому ожиданию числа одновременно занятых линий пучка.
Подставляя в (4.25) значение  , определяемое (4.21), получим
, определяемое (4.21), получим

Таким образом, интенсивность обслуженной нагрузки равна произведению интенсивности поступающей нагрузки y на вероятность того, что в пучке имеется хотя бы одна свободная линия 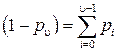 :
:
 (4.26)
(4.26)
Из (4.26) также следует, что если  , то
, то 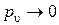 , т. е. интенсивность обслуженной нагрузки в системе без потерь равна интенсивности поступающей нагрузки. Действительно, используя (4.23), получаем
, т. е. интенсивность обслуженной нагрузки в системе без потерь равна интенсивности поступающей нагрузки. Действительно, используя (4.23), получаем
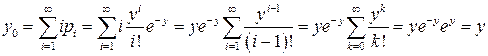
Из соотношений (4.24) и (4.26) получаем значение интенсивности потерянной нагрузки:
 (4.27)
(4.27)
Отсюда  . Следовательно, при обслуживании с потерями вызовов простейшего потока линиями полнодоступного пучка, которые включены в выходы неблокирующей коммутационной системы, вероятности потерь по времени, вызовам и нагрузке равны между собой и равны вероятности того, что пучок находится в состоянии
. Следовательно, при обслуживании с потерями вызовов простейшего потока линиями полнодоступного пучка, которые включены в выходы неблокирующей коммутационной системы, вероятности потерь по времени, вызовам и нагрузке равны между собой и равны вероятности того, что пучок находится в состоянии  :
:
 (4.28)
(4.28)
Формула потерь в полнодоступном пучке (4.28) называется первой формулой Эрланга. Функция  (или, что то же, функция
(или, что то же, функция 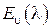 при средней длительности занятия, равной единице) табулирована. Таблицы первой формулы Эрланга построены так, что по числу линий
при средней длительности занятия, равной единице) табулирована. Таблицы первой формулы Эрланга построены так, что по числу линий  и интенсивности поступающей нагрузки у (или параметру потока l) отыскиваются потери
и интенсивности поступающей нагрузки у (или параметру потока l) отыскиваются потери  . Эти таблицы позволяют по двум любым заданным величинам из
. Эти таблицы позволяют по двум любым заданным величинам из  , у и
, у и  находить третью.
находить третью.
4.3. Обслуживание вызовов примитивного потока
Полнодоступный пучок емкостью  линий, включенных в выходы неблокирующей коммутационной системы с потерями, обслуживает вызовы, которые образуют примитивный поток с параметром
линий, включенных в выходы неблокирующей коммутационной системы с потерями, обслуживает вызовы, которые образуют примитивный поток с параметром  . Длительность обслуживания вызова коммутационной системой распределена по показательному закону
. Длительность обслуживания вызова коммутационной системой распределена по показательному закону 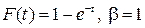 . Требуется определить вероятности различных состояний полнодоступного пучка в процессе обслуживания поступающих вызовов и вероятности потерь по времени
. Требуется определить вероятности различных состояний полнодоступного пучка в процессе обслуживания поступающих вызовов и вероятности потерь по времени  , вызовам
, вызовам  и нагрузке
и нагрузке  .
.
Примитивный поток является частным случаем симметричного потока с простым последействием. Его параметр  определяется соотношением
определяется соотношением
 (4.29)
(4.29)
где  – параметр потока вызовов свободного источника;
– параметр потока вызовов свободного источника;  – число источников вызовов, каждый из которых создает поток с одним и тем же значением параметра
– число источников вызовов, каждый из которых создает поток с одним и тем же значением параметра  . Из (4.29) следует, что параметр примитивного потока
. Из (4.29) следует, что параметр примитивного потока  пропорционален числу свободных источников, он зависит лишь от числа занятых линий пучка i.
пропорционален числу свободных источников, он зависит лишь от числа занятых линий пучка i.
Подставляя в (4.13) соотношение 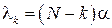 , получим:
, получим:
 ,
,
откуда
 (4.30)
(4.30)
Последняя формула называется формулой Энгсета. Она определяет вероятность  того, что в полнодоступном пучке емкостью
того, что в полнодоступном пучке емкостью  линий, который включен в неблокирующую коммутационную систему с потерями и обслуживает вызовы примитивного потока, в любой произвольный момент времени занято точно i линий, или, иными словами, вероятность того, что этот пучок находится в состоянии i.
линий, который включен в неблокирующую коммутационную систему с потерями и обслуживает вызовы примитивного потока, в любой произвольный момент времени занято точно i линий, или, иными словами, вероятность того, что этот пучок находится в состоянии i.
Естественно, что формула Энгсета (4.30) является более общей, чем формула Эрланга (4.16), и последняя может быть непосредственно получена из (4.30). Покажем это.
Число источников вызовов устремим к бесконечности  , одновременно устремив к нулю параметр одного свободного источника
, одновременно устремив к нулю параметр одного свободного источника  . При этом параметр потока вызовов всех свободных источников па сохраняем величиной конечной и постоянной –
. При этом параметр потока вызовов всех свободных источников па сохраняем величиной конечной и постоянной – 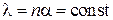 . Тогда при любом конечном значении
. Тогда при любом конечном значении 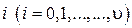
 .
.
Таким образом, при  из формулы Энгсета получается формула Эрланга.
из формулы Энгсета получается формула Эрланга.
Соотношения между параметром потока 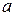 и нагрузкой, поступающей от одного источника. Рассмотрим систему без потерь, т. е. систему, в которой число линий равно числу источников
и нагрузкой, поступающей от одного источника. Рассмотрим систему без потерь, т. е. систему, в которой число линий равно числу источников  . В такой системе каждый источник может обслуживаться независимо от состояния других источников. Поэтому достаточно рассмотреть случай
. В такой системе каждый источник может обслуживаться независимо от состояния других источников. Поэтому достаточно рассмотреть случай  . При этом по (4.30) получаем:
. При этом по (4.30) получаем:  ;
;  . Вероятность
. Вероятность 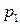 в рассматриваемом случае есть доля времени, в течение которого источник занят в системе без потерь, что численно соответствует интенсивности нагрузки
в рассматриваемом случае есть доля времени, в течение которого источник занят в системе без потерь, что численно соответствует интенсивности нагрузки 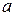 , поступающей от одного источника –
, поступающей от одного источника – 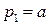 . Отсюда:
. Отсюда:
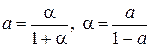 (4.31)
(4.31)
Установим соотношение между параметром потока вызовов, поступающих от одного источника в системе без потерь, и параметром потока 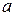 одного свободного источника. Согласно определению параметр потока есть
одного свободного источника. Согласно определению параметр потока есть  Вероятность
Вероятность  того, что за промежуток времени
того, что за промежуток времени  , от рассматриваемого источника поступит один и более вызовов, определяется произведением вероятности
, от рассматриваемого источника поступит один и более вызовов, определяется произведением вероятности  того, что в момент t источник свободен, на сумму, состоящую из вероятности того, что за промежуток времени
того, что в момент t источник свободен, на сумму, состоящую из вероятности того, что за промежуток времени  от свободного источника поступит точно один вызов (эта вероятность равна
от свободного источника поступит точно один вызов (эта вероятность равна 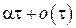 ), и вероятности поступления за этот промежуток более одного вызова (вероятность равна
), и вероятности поступления за этот промежуток более одного вызова (вероятность равна 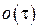 ). Поэтому
). Поэтому  , и параметр потока вызовов одного источника равен
, и параметр потока вызовов одного источника равен
 (4.32)
(4.32)
Таким образом, параметр потока вызовов одного источника численно равен интенсивности поступающей нагрузки от одного источника.
Заменим в (4.30) параметр 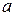 соотношением (4.31) и получим формулу Энгсета, выраженную через величину интенсивности поступающей от одного источника нагрузки
соотношением (4.31) и получим формулу Энгсета, выраженную через величину интенсивности поступающей от одного источника нагрузки 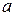 :
:

Последнюю формулу часто приводят и в другом виде:
 (4.33)
(4.33)
Если емкость пучка линий  равна числу источников
равна числу источников  , то из (4.33), в которой согласно биному Ньютона знаменатель
, то из (4.33), в которой согласно биному Ньютона знаменатель 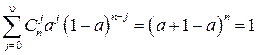 , получаем:
, получаем:
 , (4.34)
, (4.34)
т. е. вероятность того, что в произвольный момент времени из  источников занято точно i источников, определяется распределением Бернулли.
источников занято точно i источников, определяется распределением Бернулли.
Определение вероятностей потерь по времени, вызовам и нагрузке. Потери по времени  численно равны вероятности занятости всех
численно равны вероятности занятости всех  линий пучка:
линий пучка:
 (4.35)
(4.35)
Формулу для вычисления потерь по вызовам получим из соотношения (4.15), подставив в него значения параметра примитивного потока вызовов:

 (4.36)
(4.36)
Соотношения (4.30), (4.33) и (4.36) показывают, что вероятности  состояний полнодоступного пучка линий в процессе обслуживания примитивного потока вызовов, а также потери
состояний полнодоступного пучка линий в процессе обслуживания примитивного потока вызовов, а также потери  ,
,  зависят от числа источников вызовов
зависят от числа источников вызовов  , величины поступающей от одного источника нагрузки
, величины поступающей от одного источника нагрузки 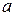 а (или параметра потока вызовов одного свободного источника
а (или параметра потока вызовов одного свободного источника  a) и емкости пучка линий
a) и емкости пучка линий  .
.
Из сопоставления (4.33) и (4.36) следует, что в полнодоступном пучке емкостью  линий, на который поступает примитивный поток вызовов, потери по вызовам при наличии
линий, на который поступает примитивный поток вызовов, потери по вызовам при наличии  источников равны потерям по времени при наличии
источников равны потерям по времени при наличии  источников, т. е.
источников, т. е. 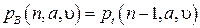 . Отсюда следует, что
. Отсюда следует, что 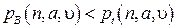 , или
, или 
Формула (4.36), определяющая потери по вызовам  , табулирована для широкого диапазона значений
, табулирована для широкого диапазона значений 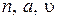 . По этим же таблицам определяют потери по времени, исходя из равенства
. По этим же таблицам определяют потери по времени, исходя из равенства  .
.
Согласно определению, вероятность потерь по нагрузке  равна отношению интенсивности потерянной
равна отношению интенсивности потерянной  к интенсивности поступающей
к интенсивности поступающей  нагрузок:
нагрузок:  .
.
Интенсивность потерянной нагрузки  есть разность интенсивностей поступающей
есть разность интенсивностей поступающей  и обслуженной
и обслуженной  нагрузок:
нагрузок:  . Интенсивность обслуженной нагрузки
. Интенсивность обслуженной нагрузки  равна математическому ожиданию числа одновременно занятых линий пучка емкостью
равна математическому ожиданию числа одновременно занятых линий пучка емкостью  :
:
 (4.37)
(4.37)
Аналогично интенсивность поступающей нагрузки  равна математическому ожиданию числа занятых линий в пучке емкостью
равна математическому ожиданию числа занятых линий в пучке емкостью  (в системе без потерь):
(в системе без потерь):

Отсюда
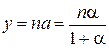 (4.38)
(4.38)
Таким образом, интенсивность поступающей нагрузки равна произведению числа источников  , создающих эту нагрузку, на интенсивность нагрузки
, создающих эту нагрузку, на интенсивность нагрузки 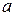 одного источника. Из соотношения (4.38) также следует, что математическое ожидание числа занятых линий
одного источника. Из соотношения (4.38) также следует, что математическое ожидание числа занятых линий  в системе без потерь составляет
в системе без потерь составляет  .
.
Используя соотношение (4.38) и (4.38), находим

Упростим числитель последней дроби; развернем значения приведенных в числителе рядов и сгруппируем все коэффициенты, относящиеся к параметру  , имеющему одну и ту же степень. В результате этого числитель преобразуется к виду
, имеющему одну и ту же степень. В результате этого числитель преобразуется к виду 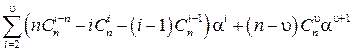 .
.
Так как  , то рассматриваемый числитель равен
, то рассматриваемый числитель равен  . Тогда
. Тогда
 .
.
С учетом (4.35) получаем формулу, определяющую потери по нагрузке:
 (4.39)
(4.39)
Из этой формулы следует, что потери по нагрузке  меньше потерь по времени
меньше потерь по времени  и даже в предельном случае, когда
и даже в предельном случае, когда  потери по нагрузке
потери по нагрузке  , а потери по времени (4.35)
, а потери по времени (4.35) 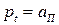 . Можно показать, что потери по нагрузке
. Можно показать, что потери по нагрузке  всегда меньше и потерь по вызовам
всегда меньше и потерь по вызовам  .
.
Таким образом, при обслуживании примитивного потока вызовов полнодоступным пучком, включенным в неблокирующую коммутационную систему, потери по нагрузке меньше потерь по вызовам, а последние меньше потерь по времени, т. е. имеет место неравенство
 (4.40)
(4.40)
При обслуживании же таким пучком простейшего потока вызовов, как было показано (4.28), между этими потерями имеет место равенство
 (4.41)
(4.41)
Дата добавления: 2015-09-10; просмотров: 193 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Министерство здравоохранения Республики Беларусь | | | Неполнодоступное включение. Системы с потерями. |