Читайте также:
|
1. Понятие множества. Подмножество. Универсальное множество. Основные способы задания множеств. Равенство и эквивалентность множеств.
2. Пересечение, объединение и разность множеств. Дополнение множества. Диаграммы Эйлера-Венна. Декартово произведение множеств.
3. Числовые множества. Числовые промежутки. Окрестность конечной точки и бесконечности.
4. Функция: определение, основные способы задания. Естественная область определения функции. Явная, неявная и параметрическая формы аналитического задания функции. График функции. Основные элементы поведения функции (чётность, нечётность, периодичность, ограниченность, монотонность).
5. Основные элементарные функции (степенные: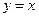 
, 
, 
, 
, 
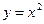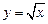; тригонометрические: 
, 
, 
, 
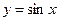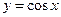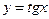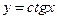; обратные тригонометрические: 
, 
, 
, 
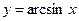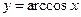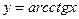; показательная 
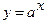, логарифмическая 
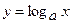), их свойства и графики.
6. Построение графиков: элементарных функций путём преобразований известных графиков; функций, содержащим знак абсолютной величины; функций, задаваемых несколькими аналитическими выражениями.
7. Понятие числовой последовательности, арифметические операции над ними. Ограниченные и неограниченные, монотонные последовательности.
8. Бесконечно малые и большие числовые последовательности, их основные свойства.
9. Определение предела числовой последовательности. Сходящиеся и расходящиеся числовые последовательности. Основные свойства сходящихся последовательностей.
10. Признаки сходимости числовых последовательностей. Последовательность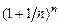 
и число 
.
11. Определения предела функции в конечной точке и на бесконечности. Односторонние пределы. Необходимое и достаточное условия существования предела функции в конечной точке.
12. Бесконечно малые функции, их основные свойства. Примеры бесконечно малых функций. Сравнение бесконечно малых функций.
13. Теорема о пределах арифметических операций над функциями, имеющими конечный предел.
14. Первый и второй замечательные пределы, их следствия и применение при вычислении пределов.
15. Эквивалентные бесконечно малые функции, их основные свойства и применение при вычислении пределов.
16. Определения непрерывности функции в точке. Понятие непрерывности справа и слева. Необходимое и достаточное условия непрерывности функции в точке. Непрерывность элементарных функций.
17. Точки разрыва функции, их классификация и нахождение.
Дата добавления: 2015-09-10; просмотров: 77 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Симптомы отравления | | | Термины для подготовки к коллоквиуму |