
Читайте также:
|
Скласти таблицю символічних імен та програму для розв’язання задачі.
Дано три числа: a,b,c. з'ясувати правильність твердження a>b та a<c.
Розв’язання.
Таблиця символічних імен
| Математичне ім’я | Ім’я у програмі | Смислове значення | Змінна | |
| Тип | Значення | |||
| a | a | Змінна для порівняння | int | Уводиться з клавіатури |
| b | b | Змінна для порівняння | int | Уводиться з клавіатури |
| c | c | Змінна для порівняння | int | Уводиться з клавіатури |
Текст програми мовою С++
для компіляторів Borland C
#include <iostream.h>
int main()
{
int a, b, c;
cout << "Уведіть a, b, c: " << endl;
cin >> a >> b >> c; // уведення даних
if ((a > b) && (a < c)) // якщо умова виконається,
cout << "a>b i a<c - Правильно!" << endl; // на екрані
// відобразиться «a>b i a<c - Правильно!»
else // якщо умова не виконається,
cout << "Неправильно a>b i a<c"<< endl; // на екрані
// відобразиться «Неправильно a>b i a<c»
return 0;
}
5. Варіанти завдань
Кожен студент вибирає варіант завдання за номером у списку групи.
Завдання. Скласти схему алгоритму, таблицю симолічних імен та програму для обчислення необхідного значення за формулою відповідного варіанта:
1. Відомі два числа. Замінити друге число нулем, якщо воно більше першого, і залишити незмінним, якщо це не так.
2. Знайти найменше з трьох відомих чисел.
3. Знайти найбільше з трьох відомих чисел.
4. Відомі три числа. Від’ємне з них число залишити без зміни, а інші – піднести до квадрата.
5. Відомі три числа  ,
,  і
і  . З'ясувати правильність умови
. З'ясувати правильність умови  . Відповідь вивести на екран у текстовій формі: «Правильно» або «Неправильно».
. Відповідь вивести на екран у текстовій формі: «Правильно» або «Неправильно».
6. Відомі два числа 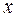 і
і 
 , менше з яких замінити їх півсумою, а більше – їхнім подвоєним добутком.
, менше з яких замінити їх півсумою, а більше – їхнім подвоєним добутком.
7. Відомі три числа  ,
,  і
і  . Якщо виконується умова
. Якщо виконується умова  , подвоїти кожне з цих чисел, а в противному разі замінити їх значення модулями.
, подвоїти кожне з цих чисел, а в противному разі замінити їх значення модулями.
8. Відомі два числа  і
і  . Якщо
. Якщо  і
і  – від’ємні, то кожне число замінити його модулем; якщо від’ємне одне з них, кожне число збільшити на 0,5; якщо
– від’ємні, то кожне число замінити його модулем; якщо від’ємне одне з них, кожне число збільшити на 0,5; якщо  і
і  – невід’ємні, кожне число збільшити в 10 разів.
– невід’ємні, кожне число збільшити в 10 разів.
9. Дано позитивні числа  ,
, 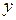 ,
,  . З'ясувати, чи існує трикутник із довжинами сторін
. З'ясувати, чи існує трикутник із довжинами сторін  ,
,  ,
,  . Відповідь вивести на екран у вигляді тексту.
. Відповідь вивести на екран у вигляді тексту.
10. Визначити, чи матиме квадратне рівняння  хоча б один дійсний розв’язок. Відповідь вивести на екран як текст.
хоча б один дійсний розв’язок. Відповідь вивести на екран як текст.
11. Знайти найбільше і найменше з двох відомих чисел.
12. Продаж книг у книгарні здійснюється за допомогою ЕОМ. Скласти програму, що запитує вартість книг; суму грошей, внесену покупцем; а потім визначає належну здачу (якщо грошей внесено більше); друкує “Спасибі за покупку!”, якщо здачі не потрібно, або видає повідомлення про нестачу внесеної суми.
13. Відомі числа  і
і 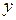 . Поміняти їх місцями так, щоб виконувалося співвідношення
. Поміняти їх місцями так, щоб виконувалося співвідношення 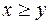 .
.
14. Відомі координати трьох точок 
 ,
, 
 і
і 
 . З'ясувати, чи лежать ці точки на одній прямій. Відповідь вивести на екран
. З'ясувати, чи лежать ці точки на одній прямій. Відповідь вивести на екран
як текст.
15. Відомі координати точки 
 . З'ясувати, чи належить точка
. З'ясувати, чи належить точка  кільцю
кільцю
з центром на початку координат із радіусами: зовнішнім  і внутрішнім
і внутрішнім 
 .
.
16. Відомі координати точки 
 . З'ясувати, чи належить точка
. З'ясувати, чи належить точка  колу одиничного радіуса з центром у точці
колу одиничного радіуса з центром у точці 
 .
.
17. На площині задані пряма 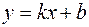 і точка
і точка 
 . З'ясувати, чи належить точка
. З'ясувати, чи належить точка  цій прямій.
цій прямій.
18. На площині задані прямі  і
і  . Визначити взаємне їх розташування на площині. Указівки: умова паралельності двох прямих
. Визначити взаємне їх розташування на площині. Указівки: умова паралельності двох прямих  ; умова перпендикулярності двох прямих
; умова перпендикулярності двох прямих  .
.
19. Відомі координати вершин трикутника 
 ,
, 
 і
і 
 . Визначити, чи трикутник рівнобедрений. При обчисленні застосувати формулу відстані між двома точками
. Визначити, чи трикутник рівнобедрений. При обчисленні застосувати формулу відстані між двома точками 
 і
і 
 :
:  .
.
20. Відомі координати вершин трикутника 
 ,
, 
 і
і 
 . Визначити, чи трикутник рівнобічний. При обчисленні застосувати формулу відстані між двома точками
. Визначити, чи трикутник рівнобічний. При обчисленні застосувати формулу відстані між двома точками 
 і
і 
 :
:
 .
.
21. Сторони трикутника задані рівняннями прямих  ,
,  і
і  . Визначити, чи трикутник прямокутний. При обчисленні застосувати умову перпендикулярності прямих
. Визначити, чи трикутник прямокутний. При обчисленні застосувати умову перпендикулярності прямих  , де
, де  і
і  – коефіцієнти прямих, заданих рівняннями
– коефіцієнти прямих, заданих рівняннями  ;
;  .
.
22. На площині задані коло радіуса  із центром у точці
із центром у точці  і точка
і точка  . З'ясувати, нележить точка
. З'ясувати, нележить точка  цьому колу, кругу чи лежить поза колом.
цьому колу, кругу чи лежить поза колом.
23. Відомі координати вершин чотирикутника 
 ,
, 
 ,
, 
 і
і 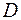
 . Визначити, чи цей чотирикутник – ромб. При обчисленні застосувати формулу відстані між двома точками
. Визначити, чи цей чотирикутник – ромб. При обчисленні застосувати формулу відстані між двома точками 
 і
і 
 :
:  .
.
24. Відомі координати вершин чотирикутника 
 ,
, 
 ,
, 
 і D
і D  . Визначити, чи цей чотирикутник – квадрат. При обчисленні застосувати формулу відстані між двома точками
. Визначити, чи цей чотирикутник – квадрат. При обчисленні застосувати формулу відстані між двома точками 
 і
і 
 :
:  .
.
25. Відомі два вектори 
 і
і 
 . Обчислити довжину цих векторів і визначити, у скільки разів вектор
. Обчислити довжину цих векторів і визначити, у скільки разів вектор  довший або коротший від вектора
довший або коротший від вектора  .
.
——————————————————————————————————————————-
Дата добавления: 2015-09-10; просмотров: 126 | Поможем написать вашу работу | Нарушение авторских прав |