Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Определение ускорений

Полное ускорение точки во вращательном движении вокруг точки О будет геометрически складываться из нормального и касательного ускорений

= + ,

Где - нормальное ускорение и направлено к центру О вращения.

- касательное ускорение, направленное по касательной к окружности радиуса ОА в сторону углового ускорения.

а_А^N=ω₁²*L_OA

а_А^N=24²*0,25=144м/c²

a_A^T=ε₁+ L_OA=0, т.к. ω₁=const. Следовательно ускорение точки А будет состоять только из одного касательного ускорения

а_А= а_А^N=144 м/c²

Масштаб плана ускорений K_a= 2 м/c²*мм.

Z_A= a_A/K_a,

Z_A=144/2=72 мм.

Для определения ускорение точки В записывается векторное уравнение, связывающее ускорение точек А и В.

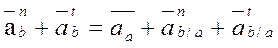
//ОА //BО //OA //AB AB

a _B/A^N=V_B/A²/L_AB

a _B/A^N =4,88²/0,8=29,829м/c²,

Z_В/A^N= a_B/A^N/K_a,

Z_B/A^N=29,829/2=14,91мм.

Из плана скоростей графически определяем неизвестные ускорения.

Z_B=36,91 мм, Z_B/A=37,58 мм, Z_B/A^T=35,44мм,

a _B/A^Т=K_a* Z_B/A^T,

a _B/A^Т=35,44*2=70,88 м/c²,

a _B=K_a* Z_B,

a _B=36,91*2=73,82 м/c²,

a _B/A=K_a* Z_B/A,

a_B/A=37,58*2=75,16 м/c²,

Определение ускорений для точек S₂ и С

Так как движение вращательное, то ускорения точек S₂ и Cпропорциональны расстояниям до осей вращения

a_S2/A= a _B/A*AS₂ /AB,

a_S2/A = 75,16*70/140=37,85 м/c²,

a_C/A= a _B/A*AC /AB,

a_C/A= 75,16*120/140=64,42 м/c²,

Z_S2/A= Z_B/A*AS₂ /AB,

Z_S2/A = 37,58*70/140=18,79мм,

Z_C/A= Z_B/A*AC /AB,

Z_C/A= 37,58*120/140=32,21мм,

Z_S2=54мм, Z_C=41,65 мм,

a_S2=K_a* Z_S2,

a _S2=54*2=108 м/c²,

a_C=K_a* Z_C,

a_C=41,65*2=83,3 м/c².

Определение ускорение точки D. Для определения ускорение точки Dзаписывается векторное уравнение, связывающее ускорение точек Cи D.

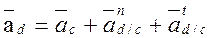
//DC DC

a _D/C^N=V_D/C²/L_DC

a _D/C^N=5,22²/0,8=34,06м/c²,

Z_D/C^N=a _D/C^N /K_a,

Z_D/C^N=34,06/2=17,03мм,

Z_D=50,5 мм Z_D/C=44,2 мм Z_D/C^T=40,79мм,

a_D=K_a* Z_D,

a_D=50,5*2=100,4м/c²,

a_D/C^T=K_a* Z_D/C^T,

a_D/C^T=40,79*2=81,6 м/c².

a_D/C=K_a* Z_D/C,

a_D/C=44,2*2=88,4 м/c².

Определение ускорения для точки S₄

a_S4/C= a_D/C*S₄C /CD,

a_S4/C=88,4*80/160=44,2м/c²,

Z_S4/C= Z_D/C*S₄C /CD,

Z_S4/C=29,6*80/160=14,8мм,

Z _S4=40,67мм

a_S4=K_a* Z_S4,

a_S4=40,67*2=81,34 м/c².

2.5 Определение угловых скоростей и ускорений

ω₂=V_B/A/L_AB,

ω₂=4,88/0,7=6,97 ед/c,

ω₄=V_D/C/L_DC,

ω₄=5,22/0,8=6,525 ед/c,

ε₂=a_B/A^T/L_AB,

ε₂=70,88/0,7=101,25 ед/c²,

ε₄=a_D/C^T/L_DC,

ε₄=81,6/0,8=102 ед/c²,

2.6. Определение сил в кинематических парах.

Главный вектор

R¹=m*a_S,

Главный момент

M=J*ε,

где J–момент инерции массы звена,

ε–угловое ускорение звена.

Главный момент и главный вектор могут быть заменены одной равнодействующей, которая смещается параллельно главному вектору на плечо

H=M/R^`*K_L,

Определение сил, приложенных к группе звеньев 4 и 5

P₀₅–давление станины 0 на направляющую 5, P₂₄ –давление звена 2 на 4

R₅=50кг*101м/с² = 5050 Н,

R₄¹=m₄*a_S4,

R₄¹=40*50,5=2020H;

M₄= J₄*ε₄,

M₄=1,2*102=122,4H*м,

H₄=M₄/R₄*K_L,

H₄=122,4/2020*0.005=12,12 мм.

h₄=H₄-10,95=1,17мм

Составим уравнение моментов относительно точки С, используя теорему Вариньона:

R₄*h₄=P₀₅*h₀₅+ P*h

P₀₅ = (-R₄*h₄ + R₅*h₅ )/ h₀₅,

P₀₅ = (-2020*1,17 + 5050*43,22)/154,9 = 1393 H.

Составим векторное уравнение сил:

R₄= Р₂₄+P₅₄+P₄₅+Р₀₅

Для построения плана задаемся масштабом сил K_p=100 H/мм и находим отрезки, пропорциональные известным силам:

y₄=R₄/K_p,

y₄=2020/100=20,2мм,

y₀₅=P₀₅/K_p,

y₀₅=1393/100=13,93мм,

Из плана сил находим y₂₄=69 мм.

P₂₄= K_p*y₂₄,

P₂₄=69*100=6900 H.

Определяем силы, приложенные к группе звеньев 2 и 3

P₀₃–давление станины 0 на ползун 3, P₁₂ –давление звена 1 на 2

R₃=m₃*a_s3,

R₃=40*36,9=1476 H

R₂¹=m₂*a_S2,

R₂¹=60*108=6480 H

P= R₃/2

P=1476/2=738 H;

M₂= J₂*ε₂,

M₂=3,6*101,2=364,52 H*м,

H₂=M₂/R₂¹*K_L,

H₂=364,52/6480*0.005=11,25мм.

Составим уравнения моментов сил относительно точки Bдля каждого звена отдельно, используя теорему Вариньона:

R₃*h₃ = -P₀₃*h₀₃ + P_t*BS₃ ,

P₀₃=(- R₃*h₃ +P_t*BS₃)/h₀₃,

P¹₀₃=(-1476*54,88+740*80)/160=-136,2 H.

P₁₂*h₁₂=-R₂*h₂+P₄₂*h₄₂

P₁₂=(-R₂*h₂+P₄₂*h₄₂)h₁₂

P¹₁₂=(-6420*65,42-67000*20)140=-3957 H

Определение неизвестных сил из плана сил. Для построения которого задаёмся масштабом К_р=50 Н/мм

y₂=R₂/K_p,

y₂=6480/50=129,6мм,

y₃=R₃/K_p,

y₃=1476/50=29,52 мм,

y=P/K_p,

y=740/50=14,8 мм,

у¹₀₃=P₀₃/K,

y₀₃=-136,2/50=2,72 мм,

P₁₂= y₁₂*K

P₁₂=174,68*50=8734 H

Определение силы, приложенной к ведущему звену:

R₁=P₂₁+P₀₁=0,

P₂₁=-P₀₁,

P₂₁=P₀₁=P₁₂=8734 H.

Определение момента сопротивления, приложенного к ведущему звену:

M₁=P₂₁*h₁*K_L,

M₁=8734 *23,9*0,005=1043,7 H*м.

2.7.Вввод

Во второй части курсовой работы мы на практике освоили методы построения плана механизма методом засечек, исходя из всех размеров его звеньев и направления движения ведущего звена. Что в свою очередь позволило нам определить скорости всех точек механизма, на основе которых мы смогли дать силовую характеристику механизма. Так как данная характеристика позволяет описать все явления в кинематических парах, она становится одной из главных задач при синтезе механизмов.

Заключение

На основании исходных данных было построено зубчатое зацепление с эвольвентным профилем зубьев. На основании измерений определено максимальное относительное скольжение, равное 0,684 м/с и коэффициент перекрытия, равный 1,288.

При исследовании шарнирно-рычажного механизма был проведен кинематический и динамический анализ.

В ходе кинематического исследования плоского шарнирно-рычажного механизма определили скорости и ускорения точек A, B, C, D, а также центров масс звеньев 2, 3 и 4. Проведя динамический анализ, определили силы действующие на звенья механизма и момент действующий на ведущее звено равный 1043,7 H*м.

Список литературы.

1. Иванов, В.А., Замалиев, А.Г. Краткий курс теории механизмов и машин: учебное пособие/В.А. Иванов, А.Г. Замалиев. –Казань: Изд-во Казанского государственного технологического университета, 2009. –160с.

2. Иванов, В.А. Статика и динамика механизмов: учебное пособие/ В.А. Иванов. –Казань; КХТИ, 1992. –72с.

3. Иванов В.А., Капотин, Б.В. Анализ и синтез механизмов: учебное пособие/ В.А. Иванов, Б.В. Капотин. –Казань; КХТИ, 1996. –64с.

4. Шитиков, Б.В. Основы теории механизмов: учебное пособие/ Б.В.Шитиков. –Казань; КХТИ, вып.4, 1971. -85с.