Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Ковариация и коэффициент корреляции случайных величин.

Ковариация — это мера линейной зависимости случайных величин.

Пусть 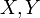— две случайные величины, определённые на одном и том же вероятностном пространстве. Тогда их ковариация определяется следующим образом:

,

в предположении, что все математические ожидания в правой части определены.

Вычисление: В силу линейности математического ожидания, ковариация может быть записана как:

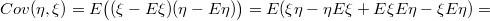
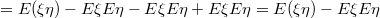
Итого,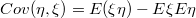

Свойства ковариации

Ковариация симметрична:

.

В силу линейности математического ожидания, ковариация может быть записана как

.

Пусть случайные величины, а 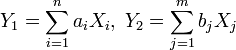их две произвольные линейные комбинации. Тогда

.

В частности ковариация (в отличие от коэффициента корреляции) не инварианта относительно смены масштаба, что не всегда удобно в приложениях.

Ковариация случайной величины с собой равна дисперсии:

.

Если 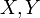независимые случайные величины, то

.

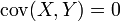Обратное, вообще говоря, неверно.

Неравенство Коши — Буняковского:

.

Коэффициент корреляции rxy случайных величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин: rxy =μxy/(σxσy)

Так как размерность μxy ровна произведению размерностей величин X и Y, σx имеет размерность величины то rxy –безразмерная величина. Таким образом, величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин. В этом состоит преимущество коэффициента корреляции перед корреляционным моментом. Очевидно, коэффициент корреляции независимых случайных величин равен нулю (т.е μxy=0).

Теорема: Абсолютная величина корреляционного момента двух случайных величин X и Y не превышает среднего геометрического их дисперсий:

| μxy|≤ квадратный корень из (DxDy)

Доказательство: Введем в рассмотрение случайную величину Z1=σyX-σxY и найдем ее дисперсию D(Z1)=2 σx^2σy^2-2 μxyσxσy

Любая дисперсия неотрицательна, поэтому 2 σx^2σy^2-2 μxyσxσy ≥0, отсюда μxy≤ σxσy

μxy≥ -σxσy отсюда - σxσy ≤ μxy ≤ σxσy (1)

т.е μxy ≤ квадратный корень из (DxDy)

Теорема: Абсолютная величина коэффициента корреляции не превышает единицы:

|rxy |≤1

Доказательство: разделим обе части двойного неравенства (1) на произведение положительных чисел σxσy:

-1 ≤rxy ≤1 т.е |rxy |≤1