Читайте также:
|
Математическим маятников называют материальную точку, совершающую колебания на невесомой нерастяжимой нити. Естественно, что математический маятник – это физическая абстракция, физическая модель. Реальным образом ее может быть принят шарик малых размеров, подвешенный на достаточно длинной нити (рис.1).
Пусть 
– длина нити маятника, т – его масса. Характеристиками, определяющими колебательное движение, можно считать или угол отклонения нити от равновесия 
или же само отклонение х, отсчитываемое по траектории движения. Если пренебречь силами сопротивления движению, то на тело маятника действуют две силы: сила тяжести 
и натяжение нити 
. В проекции на направление касательной 
уравнение движения маятника запишется так:
(1)
Знак минус возникает потому, что проекция силы противоположна направлению отклонения маятника.
При малых отклонениях маятника от положения равновесия 
. Таким образом, уравнение движения (1) запишется в виде:
. (2)
Введем обозначение 
, имеем:
. (3)
Общим решением уравнения (3) можно считать функцию
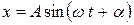. (4)
Постоянные интегрирования А и определяются из начальных условий, тогда как циклическая частота колебательного движения маятника 
. Вспомним, что период колебаний Т и их циклическая частота связаны соотношением 
. Откуда следует, что период колебаний математического маятника
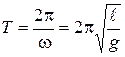. (5)
Из формулы (5) мы видим, что малые колебания маятника являются изохронными; их период не зависит от амплитуды и массы маятника. Именно это обстоятельство и позволяет использовать формулу (5) для определения ускорения силы тяжести.
Дата добавления: 2015-09-11; просмотров: 124 | Поможем написать вашу работу | Нарушение авторских прав |