Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

ВИЗНАЧЕННЯ ПРИСКОРЕННЯ ВІЛЬНОГО ПАДІННЯ ЗА ДОПОМОГОЮ МАТЕМАТИЧНОГО МАЯТНИКА ТА ПАДАЮЧОГО ЦИЛІНДРА

Мета роботи: визначення прискорення вільного падіння для даної місцевості.

Прилади і матеріали: 1) математичний маятник, 2) секундомір, 3) установка з падаючим циліндром.

1. Теоретичні відомості

Усі фізичні тіла притягуються одне до одного. Закон всесвітнього тяжіння Ньютона стверджує: дві довільні матеріальні точки притягуються одна до одної з силами, пропорційними добутку їхніх мас і обернено пропорційними квадрату відстані між ними:

Тут m₁ i m₂ – маси матеріальних точок, r – відстань між ними, а G – гравітаційна стала. G= (6,672±0,004)·10^-11 Н·м²·кг^-2.Сила взаємодій направлена вздовж прямої, що з’єднує матеріальні точки. Вже І. Ньютон показав, що сферично-симетричні тіла взаємодіють так само, як і матеріальні точки, якщо б їхні маси були зосереджені в центрах тіл.

Напруженістю гравітаційного поля називають силу, з якою поле діє на тіла масою 1 кг. Наприклад, у межах орбіти Землі Сонце створює напруженість g =5,9·10^-3 м·с^-2. Однак, внаслідок ефекту невагомості, на поверхні Землі вплив сили притягання Сонця практично відсутній. (Невагомість – це стан, при якому діючі на тіло зовнішні сили не викликають взаємних тисків його частин одна на одну. Як приклад, невагомість спостерігається при вільному поступальному русі тіла в полі тяжіння).

Земля також притягує всі тіла. На поверхні Землі сила, з якою поле тяжіння на тіло, дорівнюватиме:

Зважаючи, що маса Землі m= 5,98 10²⁴, а її середній радіус R₃= 6371 км напруженість g₀ гравітаційного полі на її поверхні дорівнюватиме:

Зі збільшенням висоти h над поверхнею Землі напруженість g зменшується. У межах тропосфери її можна визначити з формули:

На значення прискорення сили земного тяжіння впливає обертальний рух Землі, тому воно залежить від широти місця.

Значення прискорення сили тяжіння для різних широт (на висоті рівня моря)

	в		в
	978,05		980,98
	978,20		981,92
	978,65		982,61
	979,34		983,06
	980,18		983,22

1. Визначення прискорення сили земного тяжіння за допомогою математичного маятника

Одним з найпростіших прикладів гармонічного коливання є коливальний рух математичного маятника. Математичним маятником називають матеріальну точку, підвішену на невагомій і нерозтяжній нитці, що коливається у вертикальній площині під дією сили тяжіння (рис.1). З такого означення випливає, що це поняття абстрактне. До математичного маятника за своїми властивостями найбільше подібна система, що складається з нерозтяжної легкої нитки, до одного з кінців якої підвішена металева кулька. Можна вважати, що центр маси такої системи збігається з центром мас кульки.

Коли система перебуває у спокої, то сила тяжіння врівноважується силою натягу нитки N. Якщо кульку відхилити на деякий кут , то рівнодійна F сил натягу N і земного тяжіння Р намагається повернути кульку у положення рівноваги. Вертальна сила

F=mg sin . (1)

Оскільки залежність такої сили від кута нелінійна, то коливання маятника не будуть гармонічними. Для малих кутів можна записати, що і вираз вертальної сили

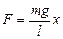(2)

де l - довжина маятника. При такій умові вертальна сила пропорційна куту, тому коливання маятника можна вважати гармонічними. Рівняння руху математичного маятника має такий вигляд:

(3)

Маса m і довжина маятника l – величини сталі для даного математичного маятника. Прискорення сили тяжіння – величина стала для даного місця на земній кулі. Тому для малих коливань силу, що повертає маятник у положення рівноваги, можна вважати квазіпружною силою:

, де .

Отже, малі коливання математичного маятника – гармонічні. Період цих коливань дорівнює

,

або . (4)

Звідси випливає, що період коливань математичного маятника не залежить від амплітуди коливань (для малих значень кута відхилень j) і маси маятника, а визначається його довжиною і прискоренням вільного падіння даного місця на Землі.

Можна довести, що в загальному випадку період коливань математичного маятника визначається формулою:

,

де - максимальний кут відхилення маятника.

Якщо =15⁰, то відносна похибка для обчислення за формулою (4) менше 0,5 %.

Спостереження над коливаннями маятників використовуються для визначення сили тяжіння. Такі спостереження мають велике значення для вивчення геологічної структури земної кори у верхніх її частинах. Наявність під землею покладів руди або нафти впливає на числове значення . Тому маятники застосовуються для геологічних розвідок цих копалин.

Хід роботи

1. Визначити час t ₁₀₀, за який відбудеться 100 повних коливань маятника.

2. Розрахувати період коливань маятника за формулою .

3. Дослід повторити тричі. Дані вимірювань і розрахунків занести в таблицю 1.

Таблиця 1.

№	t 100	T	Dt	Dt 2	l±Dl

4. Користуючись формулою (7) обчислити прискорення g вільного падіння.

5. Обчислити похибку D g вимірювання прискорення вільного падіння. Результат вимірювань записати у вигляді довірчого інтервалу

(6).

6. Визначити прискорення вільного падіння за допомогою падаючого циліндра (5). Значення g порівняйте із (6), зробіть висновки.

Методичні вказівки

Вираз для прискорення сили земного тяжіння, одержаний з формули для періоду коливань математичного маятника (4):

(7)

Логарифмуючи обидві частини цього рівняння, дістанемо:

Після диференціювання, вважаючи , знайдемо:

Замінюючи в цьому рівнянні диференціали і відповідно через абсолютні похибки i , а також змінюючи в усіх частинних диференціалах знак мінус на плюс, остаточно дістанемо таку формулу для визначення відносної похибки прискорення сили земного тяжіння:

, (8)

де і - середні абсолютні похибки вимірювань, які можна оцінювати, за допомогою інструментальної і середньої квадратичної похибок відповідно.

,

Тоді абсолютна похибка непрямого вимірювання

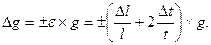(м/с²) (9)