Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Следствия.

1. Подставив значение D в условие D = ± kl, получим, что максимумы интенсивности будут наблюдаться при значениях Х, равных k = 0, 1, 2,… (5)

2. Подставив значение D в условие , получим, что максимумы интенсивности будут наблюдаться при значениях Х, равных k=0, 1, 2,. (6)

3. Шириной интерференционной полосы Dх называется расстояние между двумя соседними минимумами интенсивности. Из формулы (6) вытекает, что ширина полосы

4. Расстоянием между интерференционными полосами называется расстояние между двумя соседними максимумами. Это расстояние возрастает с уменьшением расстояния между источниками.

5. Ширина интерференционных полос и расстояние между ними зависит от длины волны l₀. Только в центре картины, при Х = 0, совпадут максимумы всех длин волн. По мере удаления от центра картины максимумы разных цветов смещаются друг относительно друга все больше и больше. Это приводит к смазыванию интерференционной картины при наблюдении ее в белом свете. В монохроматическом свете число различных полос интерференции заметно возрастает.

ДИФРАКЦИЯ СВЕТА

ДИФРАКЦИЯ СВЕТА И ПРИНЦИП ГЮЙГЕНСА – ФРЕНЕЛЯ

Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями сопоставимыми с длиной волны и связанных с отклонениями от законов геометрической оптики. Дифракция приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Между интерференцией и дифракцией нет существенного различия. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн.

Различают два вида дифракции. Если источник света S и точка наблюдения Р расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку Р, образуют практически параллельные пучки, говорят о дифракции в параллельных лучах или дифракции Фраунгофера. В противном случае говорят о д ифракции Френеля.

Принцип Гюйгенса. Каждую точку фронта волны можно рассматривать как источник вторичных волн, распространяющихся вперед по всем направлениям, в том числе и в область геометрической тени препятствия, то есть, волны должны огибать препятствия.

Принцип Френеля. 1. Можно заменить источник S₀ эквивалентной ему системой фиктивных вторичных источников и возбуждаемых ими вторичных волн. В качестве этих источников можно выбрать малые участки любой замкнутой поверхности S, охватывающей S₀.

2. Вторичные источники когерентны между собой, следовательно, должна наблюдаться интерференция света.

3. Мощности вторичного излучения равных по площади участков одинаковы. Внутрь замкнутой поверхности вторичные волны не распространяются. Если часть поверхности прикрыта непрозрачным экраном, то вторичные волны излучаются только открытыми участками.

Принцип Гюйгенса – Френеля. Каждый элемент волновой поверхности S служит источником вторичной сферической волны, амплитуда которой пропорциональна величине элемента поверхности dS и убывает с расстоянием r по закону .

МЕТОД ЗОН ФРЕНЕЛЯ

Цель. Метод зон Френеля, используя принцип Гюйгенса-Френеля, применяется для нахождения амплитуды светового колебания, возбуждаемого в точке наблюдения Р сферической волны, распространяющейся в однородной среде из точечного источника S.Волновая поверхность такой волны симметрична относительно прямой SP.

Суть метода. Френель разбил волновую поверхность на кольцевые зоны, построенные так, что расстояние от краев каждой зоны до точки Р отличается на . Из рис. видно, что расстояние b_m от внешнего края m-ой зоны до точки Р можно представить следующим образом

m = 0, 1, 2,….

где b – расстояние от вершины волновой поверхности О до точки Р.

Замечание. Колебания, приходящие в точку Р от аналогичных точек двух соседних зон, будут находится в противофазе. Поэтому и результирующие колебания, создаваемые каждой из зон в отдельности, будут для соседних зон отличаться по фазе на p.

Для оценки амплитуд колебаний нужно найти площади зон. Внешняя граница m-ой зоны выделяет на волновой поверхности сферический сегмент высоты h_m. Обозначим площадь этого сегмента S_m.. Тогда площадь m-ой зоны можно представить так

DS_m = S_m – S_m-1

где S_m-1 – площадь сферического сегмента, выделяемого внешней границей (m – 1) – ой зоны.

Из рис. следует, что

где а – радиус волновой поверхности, r_m – радиус внешней границы m – ой зоны. Возведя скобки в квадрат, получим

откуда

так как мало, то это слагаемое можно приравнять нулю, то есть . Тогда получим (1)

Площадь сферического сегмента равна S = 2×p×R×h,

где R – радиус сферы, h – высота сегмента. Следовательно,

.

А площадь m – ой зоны Френеля

(2)

Полученное выражение не зависит от m. Это означает, что при не слишком больших m площади зон Френеля примерно одинаковы.

Оценим радиусы зон Френеля. Согласно вышесказанному

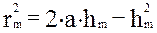
Так как при не слишком больших m высота сегмента h_m << a, то можно считать, . Подставив сюда выражение (1), найдем радиус внешней границы m – ой зоны Френеля:

(3)

Пример. Если положить a = b = 1 м и l = 0,5 мкм, то для радиуса первой (центральной) зоны получается значение r = 0,5 мкм.

Вывод. Итак, мы нашли, что площади зон Френеля примерно одинаковы. Расстояние b_m от зоны до точки Р медленной растет с увеличением номера зоны по линейному закону. Угол a между нормалью к элементам зоны и направлением на точку Р, также растет с возрастанием номера зоны. Все это приводит к тому, что амплитуда A_m колебания, возбуждаемого m – ой зоной в точке Р, монотонно убывает с ростом m. Таким образом, амплитуда колебаний, возбуждаемых в точке Р зонами Френеля, образуют монотонно убывающую последовательность.

A₁ > A₂ > A₃ > … > A_m-1 > A_m > A_m+1 > …

Фазы колебаний, возбуждаемых соседними зонами, отличаются на p. Поэтому амплитуда результирующего светового колебания в точке Р может быть найдена алгебраически:

А = А₁ – А₂ + А₃ – А₄ + … (4)

В этом выражении все амплитуды от нечетных зон входят с одним знаком, а от четных зон – с другим. Выражение (4)_ запишем в виде

(5)

Вследствие монотонного убывания A_m можно приближенно считать, что

При этом условии выражения, заключенные в круглые скобки, будут равны нулю и формула (5) упрощается

Вывод. Полученный нами результат означает, что амплитуда, создаваемая в некоторой точки Р сферической волновой поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной. То есть, действие всей волновой поверхности эквивалентно половине действия центральной зоны.

ДИФРАКЦИЯ ФРЕНЕЛЯ ОТ КРУГЛОГО ОТВЕРСТИЯ

Поставим на пути сферической световой волны непрозрачный экран с вырезанным в нем круглым отверстием радиуса r. Расположим экран так, чтобы перпендикуляр, опущенный из источника света S, попал в центр отверстия. На продолжении этого перпендикуляра возьмем точку наблюдения Р. Радиус отверстия r значительно меньше, чем расстояния a и b, r << a, b. Если а и b удовлетворяют условию (6)

где m – целое число, то отверстие оставит открытыми ровно m первых зон Френеля, построенных для точки Р. Разрешив (6) относительно m, получим число открытых зон Френеля

В соответствие с (4) амплитуда колебания в точке Р будет равна

А = А₁ – А₂ + А₃ – А₄ + … ± A_m (7)

В этом выражении амплитуда A_m берется со знаком «+», если m не четное, и со знаком «-», если m – четное.

Формулу (7) можно записать следующим образом

Выражения, заключенные в круглые скобки, можно положить равным нулю. Амплитуды от двух соседних зон мало отличаются по величине. Поэтому можно заменить через . В результате получится

где знак «+» для нечетных, а знак «-» - для четных зон.

При малых m амплитуда мало отличается от А₁. Следовательно, при нечетных m амплитуда в точке Р будет приближенно равна А₁, а при четных m – нулю.

Характер дифракционной картины. Поместим в точку Р экран, параллельный преграде с отверстиями. Вследствие симметрии преграды относительно SP, освещенность в разных точках экрана будут зависеть только от расстояния от центра дифракционной картины, помещенного в точке Р. В самой этой точке интенсивность будет достигать максимума или минимума в зависимости от того, каким – четным или нечетны – будет число открытых зон Френеля. Таким образом, дифракционная картина от круглого отверстия представляет собой чередование светлых и темнах концентрических колец.

Дифракция Фраунгофера от щели.

Дифракция плоских волн, или дифракция в параллельных лучах впервые была рассмотрена Фраунгофером в 1821 г. Для получения пучка параллельных лучей света, падающих на препятствие, обычно пользуются небольшим источником света, который помещается в фокусе собирающей линзы. Распределение по различным направлениям интенсивности света за препятствием исследуется с помощью второй собирающей линзы и экрана,

расположенного в фокальной плоскости линзы. При визуальном наблюдении вместо линзы и экрана пользуются зрительной трубой, настроенной на бесконечность. Наибольший практический интерес представляют случаи дифракции, наблюдающиеся при прохождении плоской волны сквозь узкую щель или круглое отверстие в непрозрачном экране и дифракционную решетку.

Пусть параллельный жучек монохроматического света падает нормально на непрозрачный экран Е, в котором прорезана узкая щель ВС, имеющая постоянную ширину b == ВC и длину . В соответствие с принципом Гюйгенса-Фре­неля точки щели являются вторичными источниками волн, колеблющимися в одной фазе, так как плоскость щели совпадает с фронтом падающей волны. Если бы при про­хождении света через щель соблюдался бы закон прямолинейного распространения света, то на экране Э, установленном в фокальной плоскости собирающей линзы, получалось бы изображение источника света. Вследствие дифракции на узкой щели картина коренным образом изменяется: на экране появляется система интерференционных максимумов – размытых изображений источников света, разделенных темными промежутками интерференционных минимумов.

В побочном фокусе линзы собираются все параллельные лучи, падающие на линзу под углом j к её оптической оси, перпендикулярной к фронту падающей волны. Оптическая разность хода D между крайними лучами CN и ВМ, идущими от щели в этом направлении, равна

D = CD = b×sinj

Щель ВС можно разбить на зоны Френеля, имеющие вид полос параллельных ребру щели. Ширина каждой зоны равна , так что оптическая разность хода лучей, проведенных из краев зоны параллельно ВМ, равна . Все зоны в заданном направлении излучают свет совершенно одинаково. При интерференции света от каждой пары соседних зон амплитуда результирующих колебаний равна нулю, так как это зоны вызывают колебания с одинаковыми амплитудами, но противоположными фазами. Таким образом, результат интерференции света в точке наблюдения определяется тем, сколько зон Френеля укладывается в щели. Если число зон четное

k= 1, 2, 3…

то наблюдается дифракционный минимум

Если число зон нечетное

k= 1, 2, 3…

то наблюдается дифракционный максимум, соответствующий действию одной зоны Френеля. Величина k – называется порядком дифракционного максимума.

В направлении j = 0 наблюдается самый интенсивный центральный максимум нулевого порядка: колебания возбуждаемые в точке наблюдения всеми участками щели, совершаются в одной фазе.

Дифракционная картина существенным образом зависит от отношения ширины щели b к длине волны l. В самом деле, если b = k×l, как видно из уравнения , угол j соответствующий минимуму k-ого порядка равен . Следовательно, как бы не были бы велики размеры линзы и экрана, на экране нельзя наблюдать максимумы, порядок которых больше k – 1.

Шириной дифракционного максимума на экране называется расстояние между двумя ближайшими к нему дифракционными минимумами. Ширина максимума нулевого порядка равна расстоянию между двумя минимумами первого порядка

1. Если не велико, то есть щель очень узка, то все наблюдающиеся максимумы очень широки и дифракционная картина малоконтрастная. Поток энергии через узкую щель крайне мал, так что интенсивность даже нулевого максимума очень мала.

2. Если щель широкая, то центральный максимум очень узкий и яркий и представляет собой ни что иное, как изображение на экране источника света.

3. Если щель освещать монохроматическим светом, то дифракционная картина омет окраску, соответствующую длине волны этого монохроматического света.

4. Если освещать щель белым светом, то центральный максимум имеет радужную окраску по краям. Полное гашение света не происходит ни в одной точке экрана, так как максимумы и минимумы с разной длиной волны перекрываются.

5. Если падающий пучок монохроматического света нормален к плоскости отверстия, то дифракционная картина имеет вид центрального светлого пятна окруженного системой чередующихся темный и светлых колец. Если свет падает на отверстие под небольшим углом, то характер дифракционной картины не меняется, но её центр перемещается в побочный фокус линзы.

ДИФРАКЦИОННАЯ РЕШЕТКА

Простейшая одномерная дифракционная решетка представляет собой систему из большого числа одинаковых по ширине и параллельных друг другу щелей, лежащих в одной плоскости и разделенных непрозрачными промежутками, равными по ширине. Обозначим ширину щелей через b, а ширину непрозрачных промежутков – через а. Величина d = a + b называется периодом дифракционной решетки.

При освещении решетки монохроматическим светом дифракционная картина на экране значительно сложнее, чем в случае одной щели, так как свет от разных щелей также интерферирует.

Рассмотрим дифракцию плоской монохроматической волны, падающей нормально на поверхность решетки. Колебания во всех точках щелей происходят в одной фазе, так как эти точки находятся на одной волновой поверхности. Сдвиг фаз определяется оптической разностью хода от сходственных точек двух соседних щелей до точки F_j.

D = d×sinj D = ± k×l

Тогда условием главных максимумов будет

d×sinj = ± k×l k = 0, 1,2,…

Главные минимумы соответствуют таким углам j, для которых А_j = 0, то есть свет от разных частей каждой щели полностью погашается в результате интерференции. Условие главных минимумов выражается соотношением

b×sinj = ± k×l k = 1,2,3,…

Кроме главных максимумом имеется большое число очень слабых побочных максимумов, разделенных дополнительными минимумами, которые определяются условием

где р принимает любые целые положительные значения, кроме N, 2N, 3N,…, N – число щелей решетки.

Решетка освещается белым светом. Для разных значений l положение всех главных максимумов, кроме центрального, не совпадают друг с другом. Поэтому центральный максимум имеет вид белой полоски, а все остальные радужных полосок, называемых дифракционными спектрами первого, второго и т.д. порядков. В каждой полоске у внутреннего края – фиолетовый цвет, у наружного края – красный.