Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Основные характеристики дифракционной решетки.

1. Дисперсия. Дисперсия определяет угловое или линейное расстояние между двумя спектральными линиями, отличающимися по длине волны на 10 нм, то есть характеризует степень растянутости спектра в области, вблизи данной длины волны.

1а) Угловая дисперсия. Если угловые размеры Dj малого участка, на которых приходится интервал длин волн Dl, то приближенно или

Чтобы найти угловую дисперсию решетки, продифференцируем условие главного максимума d×sinj = ± k×l

d×cosj×dj = k×dl

Откуда

1б) Линейной дисперсией называют величину

где - линейное расстояние на экране между спектральными линиями, отличающимися по длине волны на Dl.

2. Разрешающая сила (разрешающая способность). Разрешающая сила определяет минимальную разность длин волнDl, при которой эти линии воспринимаются на спектре раздельно. Эта безразмерная величина, численно равная

ДИФРАКЦИЯ НА ПРОСТРАНСТВЕННОЙ РЕШЕТКЕ

Пространственной, или трехмерной, дифракционной решеткой называется такая оптически неоднородная среда, неоднородности которой периодически повторяются при изменении всех трех пространственных координат.

Примером пространственной дифракционной решетки может служить кристаллическая решетка твердого тела. Частицы, образующие эту решетку (атомы, молекулы или ионы), играют роль упорядоченно расположенных центров, когерентно рассеивающих падающий на них свет. Пусть d₁, d₂, d₃ – периоды решетки по трем осям координат X, Y, Z, которые проведены вдоль трех ребер решетки, пересекающихся в каком-либо из её узлов. Тогда при дифракции Фраунгофера главные максимумы удовлетворяют трем соотношениям, которые вытекают из условия для дифракционных максимумов при наклонном падении на одномерную дифракционную решетку. Эти соотношения, называемые условиями Лауэ, имеют вид

d₁×(cosa - cosa₀) = ±n₁×l

d₂×(cosb - cosb₀) = ±n₂×l (1)

d₃×(cosg - cosg₀) = ±n₃×l

Здесь a₀, b₀, g₀ и a, b, g - углы между осями координат X, Y, Z и направлениями распространения соответственно падающего и дифрагировавшего света; n₁, n₂ и n₃ – целые числа, определяющие порядок максимума, l - длина волны.

Из трех углов a, b и g (соответственно a₀, b₀ и g₀) независимыми являются только два угла, так как они должны удовлетворять одному геометрическому соотношению, конкретный вид которого зависит от углов между осями координат X, Y, Z. Например, если оси координат взаимно перпендикулярны, т.е. если решетка ортогональна, то геометрическое соотношение между a, b и g имеет вид

cos²a + cos²b = cos²g = 1 (2)

При произвольно заданном направлении падения монохроматического света с заданной длиной волны l на пространственную дифракционную решетку, вообще говоря, нельзя найти значения a, b и g, которые одновременно удовлетворяли и геометрическому соотношению и трем условиям Лауэ. Единственное исключение представляет максимум нулевого порядка (n₁ = n₂ = n₃), для которого a = a₀, b = b₀, g = g₀.

Для наблюдения дифракционного максимума порядка (n₁, n₂,n₃) при заданных значениях углов a₀, b₀ и g₀ необходимо, чтобы длина волны падающего света имела вполне определенное значение. Например, в случае ортогональной решетки из (1) и (2) следует, что длина волны должна быть равна

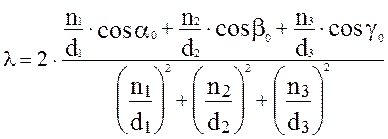(3)

Если длина волны падающего света зафиксирована, то условия Лауэ и геометрическое соотношение между углами a, b и g можно одновременно удовлетворить путем соответствующего выбора направления падения света на дифракционную решетку, т.е. углов a₀, b₀ и g₀.

Из (1) следует, что при l ³ 2d_макс где d_макс – наибольшее из значений d₁, d₂ и d₃ должны отсутствовать все дифракционные максимумы, кроме нулевого. Свет с такими длинами волн распространяется в среде, «не замечая» её неоднородности, т.е. не испытывая дифракции. Поэтому условие l ³ 2d_макс называют условием оптической неоднородности среды.

Русский физик Г.В.Вольф и английский У.Л.Брэгг независимо друг от друга предложили (1913) простой метод расчета дифракции рентгеновского излучения в кристаллах. Они исходили из предположения о том, что дифракцию рентгеновского излучения можно рассматривать как результат его отражения от системы параллельных сетчатых плоскостей кристалла, то есть плоскостей, в которых лежат узлы кристаллической решетки. Это отражение в отличие от обычного осуществляется лишь при таких условиях падения лучей на кристалл, которые соответствуют интерференционным максимумам для лучей, отраженных от разных плоскостей. На рис. показаны две соседние сетчатые плоскости кристалла АА¹ и ВВ¹. Абсолютный показатель преломления всех сред для рентгеновского излучения близок к единице, поэтому оптическая разность хода между двумя лучами!¹ и 2¹, отражающимися от плоскостей АА¹ и ВВ¹, равна

D = êDEê + êDFê= 2×d×sinq,

где d – межплоскостное расстояние, а q - угол между падающими и отраженными лучами в плоскости АА¹ (угол скольжения). Если длина волны рентгеновского излечения равна l, то интерференционные максимумы отражения удовлетворяют условию, называемому условием Вульфа – Брэгга.

2×d×sinq = n×l (4)

где n = 1, 2, 3… - порядок дифракционного максимума

Из формулы (4) следует, что наблюдение дифракционных максимумов возможно только при определенных соотношениях между длиной волны l и углом q.

Этот результат лежит в основе различных методов спектрального анализа рентгеновского излучения, то есть определения значений l по известным d и n и измеренным в опыте значениям q для дифракционных максимумов. Наиболее распространен метод качающегося (или вращающегося) кристалла. Узкий пучок исследуемого рентгеновского излучения, прошедший через отверстия в диафрагмах D₁ и D₂ направляется на кристалл К, постоянные d которого известны. В процессе покачивания (или вращения) кристалла вокруг оси О, перпендикулярной плоскости чертежа, изменяется угол q, благодаря чему обеспечивается выполнение условия (4) для всех длин волн, содержащихся в спектре анализируемого рентгеновского излучения. В качестве регистрирующего устройства используется фотопластинка. После проявления фотопластинки на ней наблюдается система дифракционных максимумов, имеющих вид темных пятен. По положению этих пятен можно найти соответствующие им значения углов q, а из формулы (4) – значение l.

С помощью дифракции рентгеновского излучения на кристаллах можно осуществлять их рентгеноструктурный анализ, то есть исследовать строение кристаллических решеток и определять межплоскостные расстояния. Эту идею впервые высказал немецкий физик М. Лауэ. Изображение монокристалла, получаемое на фотопластинке в результате дифракции узкого пучка «белого» рентгеновского излучения (с непрерывным спектром) на неподвижном кристалле, называется лауэрограммой.

В рентгеноструктурном анализе широко применяется метод исследования поликристаллических образцов. В методе Дебая – Шерера узкий пучок монохроматического рентгеновского излучения R падает на небольшой образец О, состоящий из множества мелких кристалликов, которые по-разному ориентированы относительно падающего пучка. Рентгенограмма образца, полученная на фотопластинке по методу Дебая-Шерера, называется дебаеграммой. Она представляет собой систему концентрических интерференционных колец, центры которых лежат в точке О, пересечения падающего пучка с плоскостью фотопластинки.

РАСПРОСТРАНЕНИЕ СВЕТА В ВЕЩЕСТВЕ

ВЗАИМОДЕЙСТВИЕ СВЕТА С ВЕЩЕСТВОМ

Согласно представлениям классической электронной теории, переменное электро­магнитное поле световой волны, распро­страняющейся в диэлектрической среде, вы­зывает вынужденные колебания связанных зарядов (электронов и ионов), входящих в состав молекул среды. Соответственно каждую молекулу среды можно рассмат­ривать как систему осцилляторов с различ­ными циклическими частотами собственных колебаний. Ионы значительно массивнее электронов и совершают заметные колеба­ния только под действием низкочастотного (инфракрасного) излучения. В области частот видимого и ультрафиолетового излу­чения определяющую роль играют вынуж­денные колебания внешних, наиболее слабо связанных электронов атомов и молекул, называемых оптическими электронами.

В процессе вынужденных колебаний электронов с частотой v падающего на ве­щество света периодически изменяются ди-польные электрические моменты молекул. Следовательно, молекулы излучают вторичные электромаг­нитные волны, частота которых также рав­на n. Средние расстояния между частицами вещества во много раз меньше длины коге­рентности света, поэтому вторичные волны, излучаемые весьма большим числом сосед­них молекул среды, когерентны как между собой, так и с первичной волной. При на­ложении они интерферируют, причем ре­зультат интерференции зависит от соотно­шения их амплитуд и начальных фаз.

Расчеты показывают, что в однородном изотропном веществе в результате интер­ференции образуется проходящая волна, направление распространения которой сов­падает с направлением первичной волны, а фазовая скорость зависит от частоты. В оптически неоднородной среде в результа­те наложения первичной и вторичных волн возникает рассеяние света. Наконец, при падении света на границу раздела двух различных сред в результате интерференции возникает не только проходящая, но и отраженная волна.

Вывод. Отражение света происходит не от геометрической поверхности раздела сред, а от более или менее значительного слоя частиц среды, прилегающих к границе раздела.

Поглощение света

Из опытов известно, что по мере расп­ространения плоской световой волны в ве­ществе ее интенсивность постепенно умень­шается.

Поглощением света называется явление уменьшения энергии световой волны при ее распространении в веществе, происходящее вследствие преобразования энергии электромагнитного поля волны во внутреннюю энергию вещества или в энер­гию вторичного излучения, имеющего другой спектральный состав и иные направления распространения. Поглощение света может вызывать на­гревание вещества, возбуждение и иони­зацию атомов или молекул, фотохимические реакции и другие процессы в веществе.

Еще в XVIII в. П. Бугер (1729) экспе­риментально, а И. Ламберт (1760) теорети­чески установили закон поглощения света, называемый законом Бугера — Ламберта: интенсивность плоской волны монохроматиче­ского света уменьшается по мере прохождения через поглощающую среду по экспоненциально­му закону: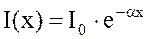

Здесь I₀ и I — интенсивности света на входе и выходе из слоя среды толщиной х; а — натуральный показатель поглощения среды, который зависит от химической природы и состояния поглощающей среды и от дли­ны волны света l и есть величина, обратная расстоянию, на ко­тором интенсивность плоской монохромати­ческой волны уменьшается в е = 2,718 раза.

Для разбавленного раствора поглощаю­щего вещества в не поглощающем раствори­теле выполняется закон Бера: а = bc, где с — концентрация раствора, а b — коэффи­циент пропорциональности, не зависящий от с. В концентрированных растворах закон Бера нарушается из-за влияния взаимодей­ствия между близко расположенными моле­кулами поглощающего вещества.

Зависимость натурального показателя поглощения диэлектрика а' от длины волны света l, характеризующая спектр погло­щения света в этой среде, связана с явлени­ем резонанса при вынужденных колебаниях электронов в атомах и атомов в молекулах диэлектрика. Диэлектрики поглощают свет более или менее селективно: поглощение велико лишь в областях частот, близких к частотам собственных колебаний электро­нов в атомах и атомов в молекулах. Наибо­лее четко это явление резонансного погло­щения света обнаруживается у разрежен­ных одноатомных газов (например, у паров большинства металлов), для которых ха­рактерен линейчатый спектр поглощения света. Дискретные частоты интенсивного поглощения света совпадают с частотами собственного излучения возбужденных ато­мов этих газов.

У газов с многоатомными молекулами наблюдаются системы тесно расположен­ных линий, образующих полосы поглоще­ния. Структура полос поглощения опреде­ляется составом и строением молекул. Жид­кие и твердые диэлектрики имеют сплошные спектры поглощения, состоящие из сравнительно широких полос поглощения, в преде­лах которых натуральный показатель по­глощения а' достигает значительной вели­чины и плавно изменяется в зависимости от длины волны l. Такой ход зависимости а' от l у конденсированных сред объясняется сильным взаимодействием между частица­ми среды, приводящим к появлению множе­ства дополнительных резонансных частот.

И С. И. Вавилов и В. Л. Лёвшин (1926) в экспериментах по поглощению света в урановом стекле обнаружили первый не­линейный эффект в оптике: оказалось, что показатель поглощения а' уранового стек­ла зависит от интенсивности I света, умень­шаясь с увеличением I. Такой характер за­висимости а' от I легко истолковывается в квантовой теории взаимодействия света с веществом. При поглощении света часть молекул среды переходит в возбужденное состояние. Эти молекулы не могут участво­вать в дальнейшем поглощении света до тех пор, пока они не вернутся, растратив свою избыточную энергию, в невозбужденное («нормальное») состояние. Доля возбуж­денных молекул среды тем больше, чем больше интенсивность света и чем больше среднее время <t> жизни молекулы в воз­бужденном состоянии. Если доля этих моле­кул незначительна, то поглощение света происходит в соответствии с законом Буге­ра — Ламберта. В противном случае а' уменьшается с ростом интенсивности света.

В. А. Фабрикант показал (1940), что можно осуществить такое неравновесное состояние вещества, при котором доля воз­бужденных молекул будет столь велика, что коэффициент поглощения вещества станет отрицательным. Это возможно, когда число актов поглощения света, пропорциональное числу невозбужденных молекул, меньше числа актов вынужденного излучения света возбужденными молекулами, пропорцио­нального числу последних. Среды с отрица­тельными коэффициентами поглощения ис­пользуются для создания квантовых генера­торов радиоволн и видимого света, на­зываемых соответственно мазерами и лазе­рами/

В заключение рассмотрим вопрос об отражении и поглощении света металлами. В газообразном состоянии металлы являют­ся диэлектриками и не обнаруживают ка­ких-либо аномальных оптических свойств. В конденсированном состоянии металлы со­держат огромное количество электронов проводимости и потому обладают высокой электрической проводимостью. Под дей­ствием света электроны проводимости со­вершают переменное движение и излучают вторичные волны. В результате наложения первичной волны, падающей на поверхность металла, и вторичных волн образуются ин­тенсивная отраженная волна и сравнитель­но слабая волна, проходящая в металл. Коэффициент отражения может достигать 0,95 и более. Он зависит от чистоты по­верхности металла, его электрической про­водимости и частоты света. Преломленная волна очень быстро поглощается в металле. Ее энергия расходуется на джоулеву тепло­ту, выделяемую токами проводимости, воз­никающими под действием света в тонком слое металла у его поверхности. В области частот инфракрасного излучения оптиче­ские свойства металлов определяются глав­ным образом электронами проводимости. Однако в области видимого света и особен­но ультрафиолетового излучения заметную роль начинают играть связанные электро­ны, находящиеся в ионах металла. Это при­водит к уменьшению коэффициента отраже­ния и заметной его зависимости от частоты.

Рассеяние света

Рассеянием света называется явление преобразования света веществом, сопро­вождающееся изменением направления распространения света и проявляющееся как несобственное свечение вещества.

Это свечение обусловлено вынужденны­ми колебаниями электронов в атомах, моле­кулах или ионах рассеивающей среды под действием падающего света. Как показал Л.И. Мандельштам, рассеяние света может возникать только в оптически неоднородной среде, показатель преломле­ния которой нерегулярно изменяется от точ­ки к точке. Примерами таких сред могут служить мутные среды - аэрозоли (дым, туман), эмульсии, коллоидные растворы, матовые стекла и т. п., содержащие мелкие частицы, показатель преломления которых отличается от показателя преломления ок­ружающей среды.

В случае оптически однородной среды ее одинаковые малые (по сравнению с кубом длины волны света) объемы, содержащие равное и притом достаточно большое число молекул, можно рассматривать как фикси­рованные в пространстве когерентные источ­ники вторичных волн. Следовательно, мож­но отвлечься от теплового движения факти­ческих источников вторичных волн — ато­мов и молекул среды, если только это движе­ние не нарушает оптической однородности среды. В такой среде рассеяние света дол­жно отсутствовать, так как для всех направ­лений, отличных от направления первичного пучка света, вторичные волны взаимно га­сятся из-за интерференции.

Иначе обстоит дело в случае оптически неоднородной среды. Если расстояние меж­ду малыми по размеру неоднородностями среды (например, между инородными частицами мутной среды) значительно больше длины волны света, то эти неодно­родности ведут себя как независимые вто­ричные источники света. Излучаемые ими волны не когерентны между собой и при наложении не могут интерферировать, по­этому оптически неоднородная среда рассе­ивает свет по всем направлениям.

Рассеяние света в мутных средах на частицах, размеры которых малы по сравне­нию с длиной волны света l, называется явлением Тиндаля. Его можно наблюдать, например, при прохождении яркого пучка света через слой воздуха, заполненный мел­кими частичками дыма, или через сосуд с водой, в которую добавлено немного моло­ка, содержащего небольшие капельки жира. Если мутная среда освещается пучком бе­лого света, то при наблюдении сбоку, т. е. в рассеянном свете, она кажется голу­боватой. В свете, прошедшем сквозь до­статочно толстый слой мутной среды, обна­руживается преобладание длинноволнового света, так что в проходящем свете среда кажется красноватой.

Для рассеянного света справедлив закон Рэлея (1899): интенсивность рассеянного света обратно про­порциональна четвертой степени длины волны: I ~ l^-4

Явление Тиндаля используется в уль­трамикроскопе для обнаружения мельчай­ших коллоидных частиц размером до 10^-9 м и наблюдения за их движением.

По мере увеличения размеров r₀ неоднородностей в мутной среде указанные выше закономерности рассеяния света постепенно искажаются. Для больших частиц, (r >> λ) наблюдается геометрическое рассеяние. В этом случае весь свет, падающий на поверхность крупной частицы рассеивается в стороны. При r > l интенсивность рассеяния вперед больше, чем назад. Это явление называется эффектом Ми. При r₀ >> l спектральный состав рассе­янного света практически совпадает со спектральным составом падающего света. Этим объясняется, например, белый цвет облаков.

Рассеяние света наблюдается также в чистых средах, не содержащих каких-либо частиц примесей (например, в чистых газах и жидкостях, истинных растворах). Оно называется молекулярным рассеянием све­та и обусловлено, как впервые предположил М. Смолуховский (1908), флуктуациями плотности, возникающими в процессе хао­тического теплового движения молекул сре­ды. Дополнительными причинами возникно­вения оптической неоднородности в чистых средах с анизотропными (полярными) мо­лекулами являются флуктуации ориентации молекул (флуктуации анизотропии), а в истинных растворах, кроме того, флук­туации концентрации. А. Эйнштейн, осно­вываясь на идее М. Смолуховского, создал теорию молекулярного рассеяния света (1910). Как показывают расчеты, размеры участков среды, соответствующих более или менее значительным флуктуациям, при обычных условиях значительно меньше длин волн видимого света.

Молекулярным рассеянием в атмосфере коротковолновой части видимого солнечно­го света объясняется голубой цвет неба. По тем же причинам при восходе и закате прямой солнечный свет, прошедший сквозь значительную толщу атмосферы, должен быть красно-оранжевым. Флуктуации плот­ности и интенсивность рассеяния света воз­растают с увеличением температуры. Этим объясняется более насыщенный цвет неба в ясный летний день по сравнению с таким же зимним днем.

Наиболее значительные флуктуации плотности в газах возникают в критическом состоянии, т. е. в состоянии, когда газ по своим свойствам становится тождественным жидкости. При этом наблюдается столь ин­тенсивное рассеяние света, называемое кри­тической опалесценцией, что даже сравни­тельно тонкий слой вещества полностью рассеивает весь падающий на него свет. Молекулярное рассеяние света происходит также и в кристаллических твердых телах. Это явление, значительно более слабое, чем рассеяние в жидкостях, впервые было обнаружено экспери­ментально Г. С. Ландсбергом (1926). Теория мо­лекулярного рассеяния света в кристаллах была разработана Л. И. Мандельштамом. Благодаря сильному взаимодействию между частицами в кристаллах флуктуации плотности, обусловливающие рассеяние света, тесно связаны с упругими свойствами всего кристалла. Случай­но возникшие флуктуации давления и связанные с ними флуктуации плотности должны распро­страняться в кристалле в виде упругих тепловых волн. Исходя из этой основной идеи, Мандель­штам пришел к выводу, что рассеяние света в кристаллах можно рассматривать как результат дифракции падающего света на упругих тепловых волнах гиперзвуковых частот.

Теория Мандельштама оказалась примени­мой не только к кристаллам, но и к аморфным твердым телам и жидкостям. Из нее следовал важный вывод о том, что при молекулярном рас­сеянии света в указанных средах должна су­ществовать тонкая структура спектра рассеянно­го света, обусловленная модуляцией света гипер­звуковыми упругими волнами. Это явление получило название рассеяния Мандельштама — Бриллюэна.

ДИСПЕРСИЯ СВЕТА

Дисперсией света называется зависимость фазовой скорости света в среде от его частоты n.

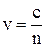Мы знаем, что , следовательно, . Так как с - универсальная постоянная, одинаковая для электромагнитных волн любой частоты, то существование дисперсии света в среде обусловлено тем, что показатель преломления среды не зависит от частоты. Эта зависимость легко обнаруживается, например, при прохождении пучка белого света через призму, изготовленную из какой-либо прозрачной среды. На экране установленном за призмой, наблюдается радужная полоска, которая называется призматическим (дисперсионным) спектром.

Зависимость показателя преломления среды n от частоты n нелинейная и немонотонная. Области значений частот, в которых , то есть с ростом частоты увеличивается и показатель преломления, соответствует нормальной дисперсии света. Нормальная дисперсия наблюдается у веществ прозрачных для света. Например, обычное стекло прозрачно для видимого света и в этой области частот наблюдается нормальная дисперсия.

Аномальной называется дисперсия света, если , то есть с ростом частоты показатель преломлении уменьшается. Аномальная дисперсия наблюдается в области частот, соответствующих полосам интенсивного поглощения света в данной среде. Например, у обычного стекла эти полосы находятся в инфракрасной и ультрафиолетовой частях спектра.

Рассмотрим взаимосвязь между фазовой и групповой скоростями. В зависимости от характера дисперсии групповая скорость u света в веществе может быть как больше, так и меньше фазовой скорости v. Покажем это.

1. Дисперсии нет. Пусть волна описывается уравнением

x = А×cos(wt – kx)

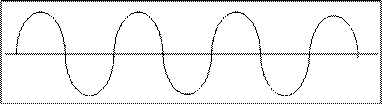и представляет собой последовательность горбов и впадин, имеющую бесконечную протяженность и длительность и определяет смещение для всех значений x и t, заключенных в пределах от -¥ до +¥. Ясно, что с помощью такой волны нельзя передать никаких сигналов. Для того, чтобы волна могла быть использована для передачи сигнала, на ней нужно сделать отмутку, скажем, оборвать ее на некоторый промежуток времени или изменить амплитуду. Однако, в этом случае волна уже не будет описываться нашим уравнением.

Возьмем фиксированное значение фазы

w×t - k×x = const

Дифференцирование этого выражения дает w×dt - k×dx = 0,

Откуда, для скорости, с которой перемещается данной значение фазы в пространстве, получается значение

Величина v называется фазовой скоростью.

Мы знаем, что монохроматический свет представляет собой наложение волн с частотами, заключенными в интервале Dw. Группой волн называется суперпозиция волн мало отличающихся друг от друга по частоте. Уравнение группы волн имеет вид

Суммируемые здесь волны отличаются друг от друга по l, а следовательно, и по k, так как . В некоторый момент времени t отличие по фазе складываемых волн в разных точках будет различно. В одних точках волны усиливают друг друга больше, а в других – меньше. В том месте, где волны в данный момент больше всего усиливают друг друга, будет наблюдаться максимум интенсивности. С течением времени этот максимум перемещается в пространстве. Сказанное можно пояснить на примере сложения двух волн с различными длинами волн. Интенсивность максимальна в точке А, где фазы обеих волн в данный момент совпадают. В точка В и С обе волны находятся в противофазе, вследствие чего, интенсивность результирующей волны минимальна.

Точку, в которой амплитуда (интенсивность) группы волн имеет максимум, называют центром группы волн. Если все составляющие группы вол распространяются с одинаковой фазовой скоростью v, то относительное расположение волн остается неизменным. Следовательно, центр группы волн также будет перемещаться в пространстве со скоростью .

2. Дисперсия есть. В этом случае центр группы волн перемещается со скоростью

так как , то и, получаем

Окончательно

Вывод. Из полученной формулы следует, что в зависимости от знака групповая скорость может быть как меньше, так и больше фазовой. В отсутствие дисперсии и групповая скорость совпадает с фазовой, (u = v). При нормальной дисперсии групповая скорость меньше фазовой (u < v). При аномальной дисперсии групповая скорость больше фазовой (u > v).

КЛАССИЧЕСКАЯ ЭЛЕКТРОННАЯ ТЕОРИЯ ДИСПЕРСИИ СВЕТА

Оптически прозрачные среды не магнитны (m» 1), так что для их показателя преломления справедлива формула

(1)

где e и c относительная диэлектрическая проницаемость и диэлектрическая восприимчивость среды.

Вывод. Дисперсию света можно рассматривать как следствие зависимости e и c от частоты n переменного электромагнитного поля света, вызывающего поляризацию среды. Для частот видимого света поляризация среды происходит только вследствие смещения оптических электронов атомов и молекул. Таким образом, поляризованность среды можно найти по формуле

где n₀ – концентрация атомов среды, - наведенный полем электрический момент атома, обусловленный смещением оптических электронов.

Пусть каждый атом содержит только один оптический электрон, тогда , где - смещение электрона из положения равновесия и поляризованность среды (2)

С другой стороны (3)

где - напряженность электрического поля световой волны.

Из формул (1), (2) и (3) видно, что для отыскания вида зависимости показателя преломления среды от частоты света нужно найти связь между смещением оптического электрона и напряженностью поля .

Оптический электрон совершает вынужденные колебания в поле световой волны под действием следующих сил:

1) - возвращающая квазиупругая сила, где m – масса электрона, w₀ – циклическая частота его свободных колебаний.

2) - сила сопротивления, пропорциональная скорости электрона.

3) - вынуждающая сила, действующая на электрон со стороны переменного электрического поля напряженности .

Колеблющийся электрон возбуждает вторичную волну, распространяющуюся со скоростью с. Вторичная волна, складываясь с первичной, образует результирующую волну. Фаза вторичной волны отличаются от фазы первичной волны. Это приводит к тому, что результирующая волна распространяется в веществе с фазовой скоростью v, отличной от скорости волн в вакууме. Различие между v и с будет тем больше, чем сильнее вынужденные колебания электронов, то есть, чем ближе частота волны к резонансной частоте электрона. Отсюда вытекает существование зависимости v от w, то есть дисперсия.

Уравнение вынужденных колебаний

Решая это уравнение, получим амплитуду и фазу вынужденных колебаний оптического электрона

Для упрощения вычислений, затуханием за счет излучения вначале будет пренебрегать. В последствие мы учтем затухание, внеся в полученные формулы соответствующие поправки.. Положив b = 0, получим

Таким образом, при отсутствие затухания электрон будет совершать под действием вынуждающей силы колебания, описываемые формулой

Учтя, что мгновенное значение напряженности электрического поля в данной точке вещества равно E(t) = E₀×cоs(w×t + j), мгновенное значение смещения электрона из положения равновесия имеет вид

В результате смещения оптического электрона из положения равновесия молекула приобретает электрический дипольный момент

Умножив на концентрацию молекул в веществе n₀, получим мгновенное значение вектора поляризации

Тогда диэлектрическая проницаемость вещества будет

И показатель преломления будет равен

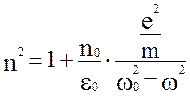
Вывод. Если частоты w₀ и w значительно отличаются друг от друга, то второе слагаемое будет мало по сравнению с единицей, так что n²» 1. При увеличения w от 0 до w₀, абсолютный показатель преломления среды монотонно возрастает от статического показателя преломления до +¥. При w₀ = w значение n скачкообразно изменяется от +¥ до -¥, а по мере увеличения w от w₀ до ¥ значение m вновь монотонно возрастает от - ¥ до 1. Такое поведение функции обусловлено тем, что мы пренебрегли затуханием. Учет затухания приводит к видоизмененной зависимости n² от w (пунктирная кривая).

ПОЛЯРИЗАЦИЯ СВЕТА

ЯВЛЕНИЕ ПОЛЯРИЗАЦИИ

Электромагнитные волны, как мы знаем, поперечны. Вместе с тем световые волны обычно не обнаруживают асимметрии относительно направления распространения. Это обусловлено тем, что в естественном свете имеются колебания, совершающиеся в самых различных направлениях, перпендикулярных к лучу. А световая волна слагается из множества цугов волн, испускаемых отдельными атомами. Плоскость колебаний для каждого цуга ориентирована случайным образом. Поэтому в результирующей волне колебания различных направлений представлены с равной вероятностью.

Поляризацией света называется выделение линейно поляризованного света из естественного или частично поляризованного.

Естественным называется свет, в котором колебания светового вектора различных направлений быстро и беспорядочно сменяют друг друга.

Поляризованным называется свет, в котором направления колебаний светового вектора упорядочены каким-либо образом.

Частично поляризованным называется свет, в котором колебания светового вектора одного направления преобладают над колебаниями других направлений.

Плоско поляризованным называется свет, в котором колебания светового вектора происходят только в одной плоскости.

Эллиптически поляризованным называется свет, если две когерентные плоско поляризованные световые волны, плоскости колебаний которых взаимно перпендикулярны, при наложении друг на друга дают волну, в которой световой вектор со временем изменяется так, что его конец описывает эллипс. При разности фаз a кратной p, эллипс вырождается в прямую и получается плоско поляризованный свет. При разности фаз a равной нечетному числу и равенстве амплитуд складываемых волн, эллипс превращается в окружность.