Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Ст.викладач Лінкова О.В.

ВИЩА МАТЕМАТИКА

КОНСПЕКТ ЛЕКЦІЙ ТА ТРЕНУВАЛЬНІ ВПРАВИ

за темою: «Визначений інтеграл»

для підготовки бакалаврів

з спеціальності 6.051001 «Метрологія та інформаційно-вимірювальні технології»

6.051002 «Метрологія, стандартизація та сертифікація»

Укладач: к.т.н. Зборовська І.А.,

ст.викладач Лінкова О.В.

Розглянуто на засіданні

кафедри загально-технічної та

фундаментальної підготовки

Протокол № 1 від 30.08 2011р

Одеса

2. Визначений інтеграл

2.1 Визначений інтеграл та його властивості

Нехай подрібнення –визначена на функція.

- довільні точки проміжків подрібнення. Сума

називається інтегральною сумою функції для подрібнення .

Зрозуміло, що вона залежить від вибору точок .

На рис. Інтегральна сума-площа заштрихованої фігури,

складеної з прямокутників. Нехай –нормальна послідовність подрібнень.

- визначена на функція, послідовність інтегральних сум. Якщо існує границя , яка не залежить від вибору нормальної послідовності , ні від вибору внутрішніх точок при утворенні інтегральних сум , то вона називається визначеним інтегралом функції на проміжку [a;b] і позначається символом . Якщо функція неперервна на [a;b],то існує.

Наприклад 1. існує, бо функція неперервна на [1;2]. Щоб обчислити цей інтеграл, візьмемо нормальну послідовність подрібнень , де . За точки беремо точки . Будуємо інтегральні суми:

Взявши до уваги, що 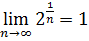і , подаємо: .

Приклад 2. Розглянемо на проміжку [0;1] функцію Діріхле:

0, якщо х-раціональне число,

1, якщо х-ірраціональне число

Нехай –довільна нормальна послідовність подрібнень [0;1]. Якщо всі точки раціональні, то , а якщо ірраціональні, то ,тому залежить від вибору точок (ця границя або дорівнює 0, або 1, або ж зовсім не існує). Отже, 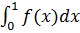не існує.

Властивості визначеного інтеграла

1. Якщо існує (функція інтегрована на [a;b], то для будь-якого числа a

2. Якщо функції і інтегровані на [a;b], то також інтегрована на [a;b] i

3. Якщо функції і інтегровані на [a;b] i для всіх , то

4. 5.

6.

7. Якщо і існують, то

.

8. Якщо функція неперервна на [a;b], то для певної точки справджується рівність .

9. Якщо неперервна на [a;b] функція і , то = для всіх .

10. Якщо функція неперервна на [a;b], то справджується формула Ньютона-Лейбніца

де –довільна первісна функції .

11. Формула інтегрування частинами.

Якщо функції і неперервні на [a;b] і мають неперервні похідні, то

Приклад 3. Обчислити

Застосовуємо властивість 11, поклавши

Матимемо:

12. Формула заміни змінної.

Якщо: функція неперервна на проміжку [ a; ] і має на цьому проміжку неперервну похідну і при умові функція неперервна на [a;b], то

Приклад 4. Обчислити

Застосовуємо заміну змінної: