
Читайте также:
|
Нехай задано швидкість руху точки V вздовж прямої OX як функція часу 
 , де t– час. Крива
, де t– час. Крива  називається графіком швидкості. Шлях S, який пройшла точка за даний проміжок часу зобразиться на графіку швидкості площею, обмеженою кривою швидкості, та віссю OX, тобто то площею
називається графіком швидкості. Шлях S, який пройшла точка за даний проміжок часу зобразиться на графіку швидкості площею, обмеженою кривою швидкості, та віссю OX, тобто то площею 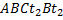 , обидві заштриховані частини б nеруться зі знаком «+», тому що
, обидві заштриховані частини б nеруться зі знаком «+», тому що 

Переміщення S точки, тобто зміна її відстані від вибраного початку розрахунку за проміжок часу  задається формулою
задається формулою 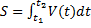 .
.
Приклад 8. Через  годин після відправлення зі станції потяг мав прискорення
годин після відправлення зі станції потяг мав прискорення  . Знайти швидкість потягу та відстань через 1 годину після відправлення, якщо, b=3, c=-42, d=80, t=1.
. Знайти швидкість потягу та відстань через 1 годину після відправлення, якщо, b=3, c=-42, d=80, t=1.
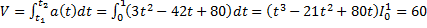 (км/год.)
(км/год.)
 (км)
(км)
Г) Обчислення довжини дуги кривої
Нехай крива задана рівнянням  (причому
(причому  неперервна разом із своєю похідною на[a;b]); тоді довжина дуги кривої визначається за формулою
неперервна разом із своєю похідною на[a;b]); тоді довжина дуги кривої визначається за формулою 

Довжина кривої, задана параметричним рівнянням  –диференційовані функції,
–диференційовані функції, 
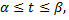 а
а 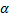 та
та  значення параметра
значення параметра  , при яких
, при яких  дорівнює
дорівнює
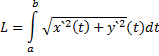
Приклад 9. Обчислити довжину кривої  на відрізку [1;4].
на відрізку [1;4].

Контрольні запитання:
1. Що називається первісною функцією для заданої функції f(x)?
2. Що називається невизначеним інтегралом від заданої функції?
3. Сформувати основні властивості невизначеного інтегралу.
4. Сформувати задачі з геометрії та фізики, які приводять до означення визначеного інтегралу.
5. Який геометричний зміст у визначеного інтегралу?
6. Сформувати основні властивості визначеного інтегралу.
7. Записати формулу Ньютона-Лейбніца.
8. Записати основну формулу заміни змінної у визначеному інтегралі.
9. Чим відрізняється метод заміни змінної у визначеному інтегралі від методу заміни змінної у невизначеному інтегралі?
10. Записати формулу обчислення площі плоскої фігури і прямокутній системі координат.
11. Записати формулу обчислення об’ємів тіл обернення.
12. Записати формулу обчислення відстані за заданою миттєвою швидкістю.
Питання для самоперевірки
1. Скільки доданків має сума  .
.
2. Як називається ця сума та від чого вона залежить?
3. Сформулюйте означення визначеного інтеграла.
4. Який геометричний та механічний зміст визначеного інтеграла?
5. Сформулюйте основні властивості визначеного інтеграла.
6. Відомо, що  . Чому дорівнює
. Чому дорівнює  .
.
7. Чому дорівнює сума  .
.
8. Якщо  , чому дорівнює
, чому дорівнює  .
.
9. Якщо  , чому дорівнює
, чому дорівнює  .
.
10. Як обчислити визначений інтеграл за формулою Ньютона-Лейбніца?
11. Поясніть формулу заміни змінної у визначеному інтегралі та інтегрування по частинах.
12. Знайдіть:

якщо функція  має рівні значення у точках
має рівні значення у точках  та неперервну похідну. Поясніть геометричний зміст отриманого результату.
та неперервну похідну. Поясніть геометричний зміст отриманого результату.
13. Відомо, що 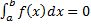 . Чи витікає з цього, що f`(x)=0 на [a;b].
. Чи витікає з цього, що f`(x)=0 на [a;b].
14. Відомо, що  неперервна та
неперервна та  . Чи витікає з цього, що
. Чи витікає з цього, що  на [a;b].
на [a;b].
15. Відомо, що  на [a;b]. Чи витікає з цього, що
на [a;b]. Чи витікає з цього, що 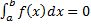 .
.
16. Відомо, що  , y=g(x) -диференційовані функції та
, y=g(x) -диференційовані функції та  на [a;b]. Чи витікає з цього, що:
на [a;b]. Чи витікає з цього, що:
А) 
Б) 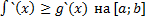 .
.
17. Визначить знак інтеграла:
А)  , якщо
, якщо  – зростаюча(спадаюча)
– зростаюча(спадаюча)
Б)  , якщо графік функції
, якщо графік функції  опуклий(впалий)на [a;b],
опуклий(впалий)на [a;b],
18.  але підінтегральна функція
але підінтегральна функція  набуває тільки додатніх значень.
набуває тільки додатніх значень.
Тренувальна робота Т-1
1. Обчислити визначені інтеграли безпосереднім інтегруванням
Приклад Відповідь
1)  8
8
2)  12
12
3)  40
40
4) 

5) 

6) 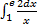 2
2
7) 

8) 

9) 

10) 

11) 

12) 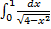

13) 
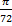
14) 

15) 

16) 

17) 

18) 
19) 

20  1
1
21) 

22) 

23) 

24) 
25) 
26)  du 1
du 1
27) 

28)  2.625
2.625
29) 

30) 

31)  1
1
32)  -1
-1
33) 

34)  1
1
35) 

36) 

37) 

38) 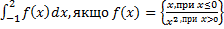

39) 

2. Не обчислюючи, визначити, який з інтегралів більший:
1)а)  б)
б)  відп(а)
відп(а)
2)а)  б)
б) 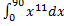 відп(б)
відп(б)
3)а)  б)
б)  відп(а)
відп(а)
4)а)  б)
б)  відп(б)
відп(б)
5)а)  б)
б)  відп(а)
відп(а)
6) а)  б)
б)  відп(а)
відп(а)
Дата добавления: 2015-09-11; просмотров: 83 | Поможем написать вашу работу | Нарушение авторских прав |