
Изучение математики вы начали с натуральных чисел, т.е. с чисел  . При сложении и умножении натуральных чисел всегда получаются натуральные числа. Однако разность и частное натуральных чисел могут не быть натуральными числами.
. При сложении и умножении натуральных чисел всегда получаются натуральные числа. Однако разность и частное натуральных чисел могут не быть натуральными числами.
Дополнением натуральных чисел нулем и отрицательными числами (т.е. числами противоположными натуральным) множество натуральных чисел расширяется до множества целых чисел, т.е. чисел вида  .При сложении, вычитании и умножении целых чисел всегда получаются целые числа. Однако частное двух целых чисел может не быть целым числом.
.При сложении, вычитании и умножении целых чисел всегда получаются целые числа. Однако частное двух целых чисел может не быть целым числом.
Введение рациональных чисел, т.е. чисел вида  , где
, где 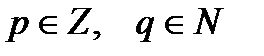 , позволило находить частное двух рациональных чисел при условии, что делитель не равен нулю. Каждое целое число
, позволило находить частное двух рациональных чисел при условии, что делитель не равен нулю. Каждое целое число  также является рациональным, так как его можно представить в виде
также является рациональным, так как его можно представить в виде  .
.
При выполнении четырех арифметических действий (кроме деления на нуль) над рациональными числами всегда получаются рациональные числа.
Если рациональное число можно представить в виде дроби  , где
, где  , то его можно записать в виде конечной десятичной дроби. Например, число
, то его можно записать в виде конечной десятичной дроби. Например, число  можно записать так
можно записать так  .
.
Существуют рациональные числа, которые нельзя записать в виде конечной десятичной дроби, например  . Если, например, попытаться записать число
. Если, например, попытаться записать число  в виде десятичной дроби, используя известный алгоритм деления уголком, то получится бесконечная десятичная дробь
в виде десятичной дроби, используя известный алгоритм деления уголком, то получится бесконечная десятичная дробь  . Бесконечную десятичную дробь
. Бесконечную десятичную дробь  называют периодической, повторяющуюся цифру
называют периодической, повторяющуюся цифру  - ее периодом. Периодическую дробь
- ее периодом. Периодическую дробь  коротко записывают так
коротко записывают так 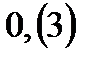 ; читается: «Ноль целых и три в периоде».
; читается: «Ноль целых и три в периоде».
Вообще, периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или несколько цифр – период дроби. Например, десятичная дробь  периодическая с периодом
периодическая с периодом  ; читается «23 целых, 14 сотых и 56 в периоде».
; читается «23 целых, 14 сотых и 56 в периоде».
Задача 1. Записать число  в виде бесконечной десятичной дроби.
в виде бесконечной десятичной дроби.
Решение. Воспользуемся алгоритмом деления уголком:

Остатки повторяются, поэтому в частном повторяется одна и та же группа цифр: 45. Следовательно,  .
.
Вообще при делении целого числа  на натуральное число
на натуральное число  на некотором шаге остаток может стать равным нулю или остатки начинают повторяться так как каждый из остатков меньше
на некотором шаге остаток может стать равным нулю или остатки начинают повторяться так как каждый из остатков меньше  . Тогда начинают повторяться и цифры частного.
. Тогда начинают повторяться и цифры частного.
В первом случае в результате деления получается целое число или конечная десятичная дробь, во втором случае – бесконечная десятичная периодическая дробь. Например: 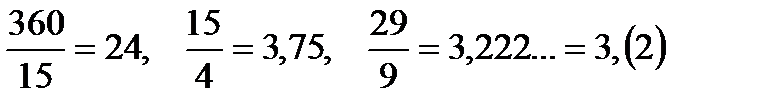 .
.
Заметим, что каждое целое число или конечную десятичную дробь можно считать и бесконечной десятичной периодической дробью с периодом, равным нулю. Например: 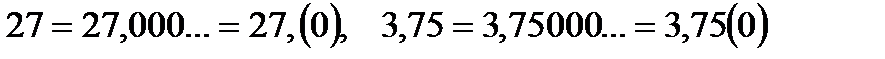 .
.
Дата добавления: 2015-09-12; просмотров: 172 | Поможем написать вашу работу | Нарушение авторских прав |