Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Многочлены Чебышева

Пусть . Рассмотрим функцию вида:

(9)

При :

При : ,

При используем тригонометрическое тождество

Пусть многочлен степени 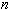. Получим рекурентное соотношение, связывающее .

Сложим почленно эти равенства и перенесем в другую сторону. Получим

(10)

Полагая в (10) , получим

(11)

Из (11) следует, что многочлен степени . Коэффициент при равен .

Корни многочлена Чебышева :

(12)

Формула (12) дает 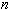различных значений при . Значение при других значениях совпадает с одним из значений из указанных. Например, при получаем то же значение, что и при:

Значения при совпадают со значениями при и т.д.

на отрезке [-1,1] равен 1. Он достигается в точках, когда

.

, (13)

Покажем, что среди всех многочленов степени n со старшим коэффициентом 1 многочлен наименее отклоняется от нуля на отрезке [-1,1].

Покажем, что для любого со старшим коэффициентом 1

.

Разность есть многочлен степени . В точках принимает поочередно значения +1, -1. Если , то разность в точках будет принимать поочередно положительные и отрицательные значения и будет иметь 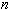нулей (между значениями ). Получаем противоречие.