|
Читайте также: |
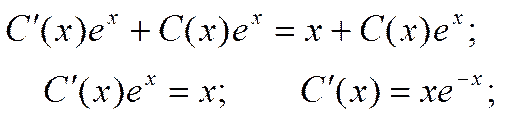
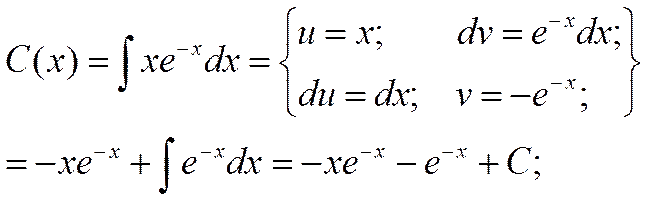
Общее решение: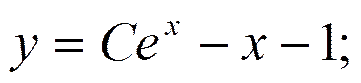 
C учетом начального условия:
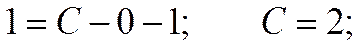
Частное решение: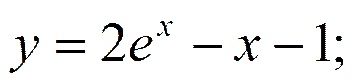 
Решим этот же пример методом Эйлера.
Применяем формулу
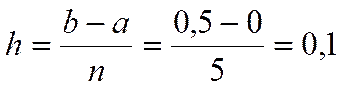
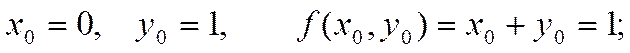
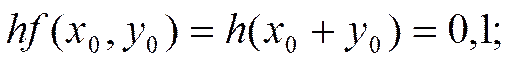
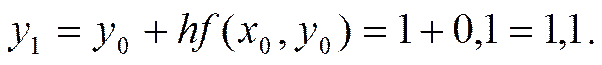
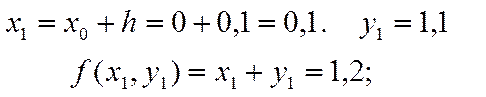
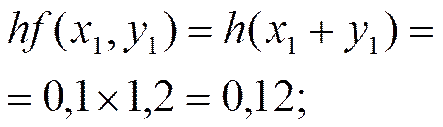
Производя аналогичные вычисления далее, получаем таблицу значений:
| k | ||||||
| Xk | 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| Yk | 1,1 | 1,22 | 1,362 | 1,528 | 1,721 |
Уточненный метод Эйлера
Для сравнения полученных результатов составим таблицу.
| k |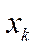 
| 
| |||
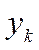
| Метод Эйлера | Уточненный метод Эйлера | Точное значение | |||
| 0,1 | 1,1 | 1,11 | 1,1103 | ||
| 0,2 | 1,22 | 1,242 | 1,2428 | ||
| 0,3 | 1,362 | 1,398 | 1,3997 | ||
| 0,4 | 1,528 | 1,581 | 1,5837 | ||
| 0,5 | 1,721 | 1,794 | 1,7975 |
Следует обратить внимание на то, ошибка (расхождение между точным и приближенным значениями) увеличивается с каждым шагом вычислений.
Это обусловлено тем, что во–первых, полученное приближенное значение округляется на каждом шаге, а во–вторых, – тем, что в качестве основы вычисления принимается значение, полученное на предыдущем шаге, т.е. приближенное значение.
Таким образом происходит накопление ошибки.
Дата добавления: 2014-12-15; просмотров: 101 | Поможем написать вашу работу | Нарушение авторских прав |