Нахождение кратчайшего пути в графе с ребрами произвольной длины.

Читайте также:

Название операции: ______________________________________________________

_________________________________________________________________________

Предоперационная подготовка больного: ___________________________________

_________________________________________________________________________

Оснащение:

хирургический инструментарий

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

перевязочный материал

растворы

Оценка принимаемых лекарств

Ф.И.О._________________________________________________________________

Диагноз________________________________________________________________

Характер препарата	I	II
Название
Группа препаратов
Фармакологическое действие
Показания
Противопоказания
Способ применения
Особенности применения (введения)

Диета (вариант) _________

Показания

Назначение

Характеристика

Фитотерапия

Лекарственные растения, обладающие направленным действием

и рекомендуемые больному

Нахождение кратчайшего пути в графе с ребрами единичной длины (или с ребрами равной длины).

a) Приписываем конечной вершине индекс 0.

b) Помечаем 1 все смежные вершины.

c) Находим все вершины, смежные вершинам, имеющим индекс 1, и приписываем им индекс 2.

d) И т.д., пока не будут помечены все вершины. Значение индекса начальной вершины будет длиной пути.

Нахождение кратчайшего пути в графе с ребрами произвольной длины.

1) Каждая вершина x_i помечается индексом _i. Конечной вершине приписываем

индекс ₀=0. Для остальных вершин предварительно полагаем _i = (i ).

2) Ищем такую дугу (x_i, x_j), для которой _i - _j > l (u_ij), и заменяем индекс _j индексом _j’ = _i + l (u_ij) < _j. Продолжаем этот процесс замены индексов до тех пор, пока остается хотя бы одна дуга, для которой можно уменьшить _j.

Если какую–то вершину можно пометить несколькими способами, то выбирается наименьшее значение.

Сформулируем правило для нахождения кратчайшего пути:

Пусть x_n =a – начальная вершина с индексом _n. Ищем вершину x_p₁, такую, что _n - _p₁ = l (u_n_,_p₁). Далее ищем вершину x_p₂, такую, что

_p₁ - _p₂ = l (u_p_1,_p₂) и т.д. до тех пор, пока не дойдем до конечной вершины.

Пример: 0 **

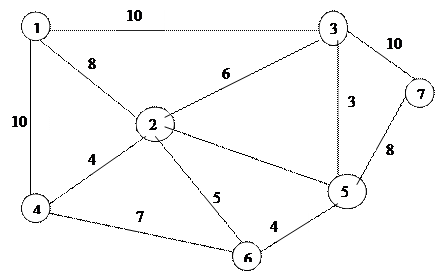
Найти кратчайший путь из вершины 6 в вершину 1.

1. Вершине 1 присваиваем индекс «0». Для остальных вершин полагаем _i = .

2. Ищем дугу, для которой _j - ₁> l (x_j,x₁). Это дуги (x₁, x₂) и (x₁, x₃).

3. Приписываем вершинам 2 и 3 индексы ₂^’ = ₁+ l (x₀,x₂) = 0 + 2 = 2; ₃^’= ₁+ l (x₀,x₃) = 0 + 9 = 9.

4. Далее ищем дуги, для которых _j - ₂ > l (x_j, x₂); _j - ₃ > l (x_j, x₃).

5. Вершинам 4, 5 приписываем индекс ₄^’ = ₂ + l (x₂, x₄) = 2 + 3 = 5,

₅^’= ₂+ l (x₂, x₅) = 2 + 3 = 5. Вершине 6 приписываем индекс

₆^’= ₃ + l ( x₃,x₆) = 9 + 7 = 16.

6. Вершину 6 можно пометить из вершины 4, так как ₆ - ₄ > l (x₄, x₆);

16–5 > 6; ₆^’ = ₄ + l (x₄, x₆) = 5 + 6 = 11.

Находим кратчайший путь. Индекс вершины 6 равен 11, значит, длина кратчайшего пути равна 11. Ищем вершину, для которой ₆ - _j = l (x₆, x_j). Это вершина 4: 11 – 6 = 5. Значит, первой промежуточной вершиной на пути 6 – 1 является вершина 4. Далее ищем вершину, для которой ₄ - _j = l (x₄, x_j). Это вершина 2: 5 – 2 = 3. И так далее, пока не дойдем до вершины 1.

Получаем кратчайший путь из вершины 6 в вершину 1: 6 – 4 – 2 – 1, длина которого равна индексу вершины 6, т.е. равна 11.

Приложение.

Дата добавления: 2014-12-15; просмотров: 144 | Поможем написать вашу работу | Нарушение авторских прав

<== предыдущая лекция	\|	следующая лекция ==>
Температура ______________	\|	Приложение 3

lektsii.net - Лекции.Нет - 2014-2025 год. (0.011 сек.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав