Произведение матриц AB состоит из всех возможных комбинаций скалярных произведений строк матрицы A и столбцов матрицы B. Элемент матрицы AB с индексами i, jесть скалярное произведение i -ой строки матрицы A и j -го столбца матрицы B.
Иллюстрация справа демонстрирует вычисление произведения двух матриц A и B, она показывает как каждые пересечения в произведении матриц соответствуют строкам матрицы A и столбцам матрицы B. Размер результирующей матрицы всегда максимально возможный, то есть для каждой строки матрицы A и столбца матрицы B есть всегда соответствующее пересечение в произведении матрицы.
Значения на пересечениях отмеченных кружочками будут:
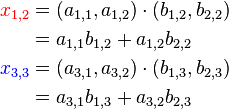
В общем случае, произведение матриц не является коммутативной операцией. К примеру:
Элемент 
произведения матриц приведённых выше вычисляется следующим образом
Первая координата в обозначении матрицы обозначает строку, вторая
координата — столбец; этот порядок используют как при индексации, так и при обозначении размера. Элемент 
на пересечении строки 
и столбца 
результирующей матрицы является скалярным произведением -й строки первой матрицы и -го столбца второй матрицы. Это объясняет почему ширина и высота умножаемых матриц должны совпадать: в противном случае скалярное произведение не определено.
Дата добавления: 2015-01-30; просмотров: 25 | Поможем написать вашу работу | Нарушение авторских прав |