
Читайте также:
|
В 1990 Копперсмит и Виноград[6] опубликовали алгоритм, умножающий матрицы со сложностью O(n2.3727). [7] Этот алгоритм использует идеи, схожие с алгоритмом Штрассена. На сегодняшний день алгоритм Копперсмита-Винограда является наиболее асимптотически быстрым, но он эффективен только на очень больших матрицах и поэтому не применяется.
Алгоритмы с использованием теории групп (2003)
В 2003 Кох и др. рассмотрели в своих работах[8] алгоритмы Штрассена и Копперсмита-Винограда в контексте теории групп. Они показали возможность существования алгоритмов умножения матриц со сложностью Θ(n2) [9].
3.
Рассмотрим квадратную матрицу
 .
.
Обозначим Δ =det A.
Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если Δ = 0.
Квадратная матрица В есть обратная матрица для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.
Теорема. Для того, чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Обратная матрица матрице А, обозначается через А-1, так что В = А-1 и вычисляется по формуле
 , (1)
, (1)
где А i j - алгебраические дополнения элементов a i j матрицы A..
Вычисление A-1 по формуле (1) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить A-1 с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ранга матрицыможно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
Пример 2.10. Для матрицы  найти A-1.
найти A-1.
Решение. Находим сначала детерминант матрицы А
 значит, обратная матрица существует и мы ее можем найти по формуле:
значит, обратная матрица существует и мы ее можем найти по формуле:  , где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы.
, где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы. 
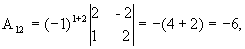




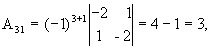


откуда  .
.
Пример 2.11. Методом элементарных преобразований найти A-1 для матрицы: А= 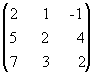 .
.
Решение. Приписываем к исходной матрице справа единичную матрицу того же порядка:  . С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей.
. С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей.
Для этого поменяем местами первый и второй столбцы:  ~
~  . К третьему столбцу прибавим первый, а ко второму - первый, умноженный на -2:
. К третьему столбцу прибавим первый, а ко второму - первый, умноженный на -2: 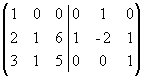 . Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 6 второй;
. Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 6 второй;  . Прибавим третий столбец к первому и второму:
. Прибавим третий столбец к первому и второму:  . Умножим последний столбец на -1:
. Умножим последний столбец на -1:  . Полученная справа от вертикальной черты квадратная матрица является обратной матрицей к данной матрице А. Итак,
. Полученная справа от вертикальной черты квадратная матрица является обратной матрицей к данной матрице А. Итак,
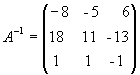 .
.
4.
2.5. Определители матриц и их свойства
Квадратную матрицу  порядка n можно сопоставить с числом
порядка n можно сопоставить с числом  (или
(или  , или
, или  ), называемым определителем или детерминантом.
), называемым определителем или детерминантом.
Вычисление определителя:
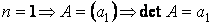 ;
;
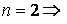
 ,
,
т. е. правило:
 ;
;


т. е. Правило треугольника (или Саррюса):
 .
.
Отметим следующие свойства определителей:
– определители не изменяются, если его строки заменить столбцами и наоборот (строки и столбцы это ряд определителя);
– при перестановке двух параллельных рядов определитель меняет знак;
– определитель, имеющий два одинаковых ряда, равен нулю;
– общий множитель элементов какого-либо рода определителя можно вынести за знак определителя;
– если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму соответственных определителей;
– определитель не изменяется, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число;
Дальнейшие свойства связаны с понятием минора и алгебраического дополнения.
5.
Миноры и алгебраические дополнения.
Определение. Минором элемента  определителя
определителя  – го порядка называют определитель
– го порядка называют определитель  – го порядка, который получается из данного определителя вычеркиванием
– го порядка, который получается из данного определителя вычеркиванием  - й строки и
- й строки и  – го столбца, на пересечении которых стоит элемент
– го столбца, на пересечении которых стоит элемент  .
.
Обозначение:  .
.
Определение. Алгебраическим дополнением элемента  определителя
определителя  – го порядка называют его минор, взятый со знаком плюс, если
– го порядка называют его минор, взятый со знаком плюс, если  – четное число и со знаком минус в противном случае.
– четное число и со знаком минус в противном случае.
Обозначение:  .
.
Пример. В определителе 3 – го порядка
 .
.
найти все миноры и алгебраические дополнения элементов второго столбца.
Решение.
 ,
,  ,
,
 ,
,  ,
,
 ,
,  .
.
Ответ:
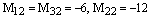 ,
,  .
.
Дата добавления: 2015-01-30; просмотров: 154 | Поможем написать вашу работу | Нарушение авторских прав |