
Описанное правило матричного умножения прозрачнее всего мотивируется исходя из умножения вектора на матрицу.
Последнее естественно вводится исходя из того, что при разложении векторов по базису действие (любого) линейного оператора A дает выражение компонент вектора v' = A v:

-то есть линейный оператор оказывается представлен матрицей, векторы - векторами-столбцами, а действие оператора на вектор - матричным умножением вектора-столбца слева на матрицу оператора (это частный случай матричного умножения, когда одна из матриц - вектор-столбец - имеет размер 1х n).
(Равно переход к любому новому базису при смене координат представляется полностью аналогичным выражением, только  в этом случае уже не компоненты нового вектора в старом базисе, а компоненты старого вектора в новом базисе; при этом
в этом случае уже не компоненты нового вектора в старом базисе, а компоненты старого вектора в новом базисе; при этом  - элементы матрицы перехода к новому базису).
- элементы матрицы перехода к новому базису).
Далее, рассмотрев последовательное действие на вектор двух операторов:
сначала A, а потом B (или преобразование базиса A, а затем преобразование базиса B), имеем, дважды применив нашу формулу:

откуда видно, что композиции BA действия линейных
операторов A и B (или аналогичной композиции преобразований базиса) соответствует матрица, вычисляемая по рецепту произведения соответствующих матриц:

Определенное таким образом произведение матриц оказывается совершенно естественным и очевидно полезным (дает простой и универсальный способ вычисления композиций произвольного количества линейных преобразований).
[править]Свойства
Сочетательное свойство:
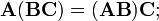

Распределительное свойство:

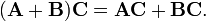 .
.
Произведение матрицы на единичную матрицу  подходящего порядка равно самой матрице:
подходящего порядка равно самой матрице:


Произведение матрицы на нулевую матрицу  подходящей размерности равно нулевой матрице:
подходящей размерности равно нулевой матрице:


Если  и
и  — квадратные матрицы одного и того же порядка, то произведение матриц обладает ещё рядом свойств.
— квадратные матрицы одного и того же порядка, то произведение матриц обладает ещё рядом свойств.
Умножение матриц в целом некоммутативно:

Если  , то матрицы
, то матрицы  и
и  называются перестановочными или коммутирующими между собой.
называются перестановочными или коммутирующими между собой.
Определитель и след произведения не зависят от порядка умножения матриц:
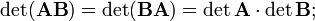
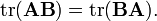
Дата добавления: 2015-01-30; просмотров: 91 | Поможем написать вашу работу | Нарушение авторских прав |
|