Читайте также:
|
Кинетическая энергия тела зависит от его скорости и массы. Например, чем больше скорость падения воды в реке и чем больше масса этой воды, тем сильнее будут вращаться турбины электростанций.
mv2
Ek = ——
2
Ek – кинетическая энергия; m – масса тела; v – скорость движения тела.
В природе, технике, быту один вид механической энергии обычно превращается в другой: потенциальная в кинетическую и кинетическая в потенциальную.
Например, при падении воды с плотины ее потенциальная энергия превращается в кинетическую. В качающемся маятнике периодически эти виды энергии переходят друг в друга.
14 Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системыможет быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.
15 Удар, или соударение, – это столкновение двух или более тел, при котором взаимодействие длится очень короткое время.
Силы взаимодействия между сталкивающимися телами столь велики, что внешними силами, действующими на них, можно пренебречь. Это позволяет систему тел в процессе столкновения рассматривать как замкнутую систему и применять к ней законы сохранения. Сущность удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара имеет место перераспределение энергии между соударяющимися телами, а относительная скорость тел после удара не достигает своего прежнего значения. Это объясняется тем, что нет идеально упругих тел и идеально гладких поверхностей.
ОПРЕДЕЛЕНИЕ: Отношение нормальных составляющих относительной скорости тел после и до удара называется коэффициентом восстановления ε.
Если для сталкивающихся тел ε = 0, то такие тела называются абсолютно неупругими, если ε = 1, то – абсолютно упругими. На практике для всех тел имеем выражение:
0 < ε < 1
(ε≈ 0,56 для стальных шаров, ε≈ 0,89 для шаров из слоновьей кости и ε≈ 0 для свинца). Однако, в некоторых случаях тела можно считать либо абсолютно упругими, либо абсолютно неупругими.
Удар называется центральным, если тела до удара движутся вдоль прямой, проходящей через их центры масс.
Абсолютно упругий удар – это столкновение двух тел, в результате которого полная механическая энергия тел сохраняется.
Для абсолютно упругого удара выполняется закон сохранения импульса и закон сохранения механической энергии (кинетической энергии). Обозначим скорости шаров массами m1 и m2 до удара через v1 и v2, после удара –v1′ и v2′. В случае прямого центрального удара векторы скоростей шаров лежат на прямой линии, соединяющей их центры. Для взаимодействующих тел имеем:
Вывод этих формул разобрать самостоятельно.
Абсолютно неупругий удар – это столкновение двух тел, в результате которого они объединяются, двигаясь дальше как одно целое.
Если массы шаров m1 и m2, их скорости до удара v1 и v2, то, используя закон сохранения импульса, можем записать:
16 Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
,
где:
· mi — масса i -й точки,
· ri — расстояние от i -й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, какмасса тела является мерой его инертности в поступательном движении.
,
где:
· 
— масса малого элемента объёма тела 
,
· 
— плотность,
· 
— расстояние от элемента до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
17 Основные кинематические характеристики вращательного движения тела — его угловая скорость (
) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:
и кинетическая энергия
где Iz — момент инерции тела относительно оси вращения.
Похожий пример можно найти при рассмотрении вращающейся молекулы с главными осями инерции I1, I2 и I3. Вращательная энергия такой молекулы задана выражением
где ω1, ω2, и ω3 — главные компоненты угловой скорости.
В общем случае, энергия при вращении с угловой скоростью 
находится по формуле:
, где 
— тензор инерции.
18 Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторнаяфизическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
19 Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).
Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.
Момент импульса замкнутой системы сохраняется.
Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю.
В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.
20 Деформа́ция (от лат. deformatio — «искажение») — изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Обычно деформация сопровождается изменением величин межатомных сил, мерой которого является упругое механическое напряжение. Деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести). Упругие деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия(другими словами, атомы не выходят за пределы межатомных связей); в основе необратимых — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия (то есть выход за рамки межатомных связей, после снятия нагрузки переориентация в новое равновесное положение).
Пластические деформации — это необратимые деформации, вызванные изменением напряжений. Деформации ползучести — это необратимые деформации, происходящие с течением времени. Способность веществ пластически деформироваться называется пластичностью. При пластической деформации металла одновременно с изменением формы меняется ряд свойств — в частности, при холодном деформировании повышается прочность.
21 Жидкости и газы передают по всем направлениям приложенное к ним давление. Об этом гласит закон Паскаля и практический опыт.
Но существует еще и собственный вес, который тоже должен влиять на давление, существующее в жидкостях и газах. Вес собственных частей или слоев. Верхние слои жидкости давят на средние, средние на нижние, а последние – на дно. То есть мы можем говорить о существовании давления столба покоящейся жидкости на дно.
Формула для расчета давления столба жидкости высотой h имеет следующий вид:
p=ρgh,
где ρ – плотность жидкости,
g – ускорение свободного падения,
h - высота столба жидкости.
Это формула так называемого гидростатического давления жидкости.
Гидростатическое давление, то есть, давление, оказываемое покоящейся жидкостью, на любой глубине не зависит от формы сосуда, в котором находится жидкость. Одно и то же количество воды, находясь в разных сосудах, будет оказывать разное давление на дно. Благодаря этому можно создать огромное давление даже небольшим количеством воды.
Это очень убедительно продемонстрировал Паскаль в семнадцатом веке. В закрытую бочку, полную воды, он вставил очень длинную узкую трубку. Поднявшись на второй этаж, он вылил в эту трубку всего лишь одну кружку воды. Бочка лопнула. Вода в трубке из-за малой толщины поднялась до очень большой высоты, и давление выросло до таких значений, что бочка не выдержала. То же самое справедливо и для газов. Однако, масса газов обычно намного меньше массы жидкостей, поэтому давление в газах, обусловленное собственным весом можно часто не учитывать на практике. Но в ряде случаев приходится считаться с этим. Например, атмосферное давление, которое давит на все находящиеся на Земле предметы, имеет большое значение в некоторых производственных процессах.
Благодаря гидростатическому давлению воды могут плавать и не тонуть корабли, которые весят зачастую не сотни, а тысячи килограмм, так как вода давит на них, как бы выталкивая наружу. Но именно по причине того же гидростатического давления на большой глубине у нас закладывает уши, а на очень большую глубину нельзя спуститься без специальных приспособлений – водолазного костюма или батискафа. Лишь немногие морские и океанические обитатели приспособились жить в условиях сильного давления на большой глубине, но по той же причине они не могут существовать в верхних слоях воды и могут погибнуть, если попадут на небольшую глубину.
22 Закон (уравнение) Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:
Здесь
— плотность жидкости,
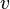— скорость потока,
— высота, на которой находится рассматриваемый элемент жидкости,
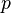— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
— ускорение свободного падения.
В научной литературе закон Бернулли, как правило, называется уравнением Бернулли [1](не следует путать с дифференциальным уравнением Бернулли), теоремой Бернулли [2][3] или интегралом Бернулли [4][5].
Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.
Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смыслкинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давления (см. приводимый в приложении вывод уравнения Бернулли) и не представляет собой запаса какого-либо специального вида энергии («энергии давления»[6]).
Соотношение, близкое[7] к приведенному выше, было получено в 1738 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.
Для горизонтальной трубы 
и уравнение Бернулли принимает вид: 
.
Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности : 
.
Согласно закону Бернулли, полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.
Полное давление состоит из весового 
, статического 
и динамического 
давлений.
Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причинойэффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров(например труба Вентури), водо- и пароструйных насосов. А последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики.
Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю. Для описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, учитывающих потери на местных и распределенных сопротивлениях.
23 Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла работы, затрачиваемой на это перемещение.
Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.
Различают динамическую вязкость (единицы измерения: Па·с = 10 Пуаз) и кинематическую вязкость (единицы измерения: Стокс, м²/с, внесистемная единица — градус Энглера). Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объёма через калиброванное отверстие под действием силы тяжести. Прибор для измерения вязкости называется вискозиметром.
1. Метод Стокса. Этот метод определения вязкости основан на измерении скорости медленно движущихся в жидкости небольших тел сферической формы.
На шарик, который падает в жидкости вертикально вниз, действуют три силы: сила тяжести Р=(4/3);πr3ρg (ρ - плотность шарика), сила Архимеда FA=(4/3);πr3ρ'g (ρ' - плотность жидкости) и сила сопротивления, эмпирически установленная Дж. Стоксом: F=6πηrν, где r - радиус шарика, ν - его скорость. При равномерном движении шарика P=FA+F или
откуда
Измерив скорость равномерного движения шарика, можно определить вязкость жидкости (газа).
Закон Пуазёйля (иногда закон Хагена — Пуазёйля) — это физический закон так называемого течения Пуазёйля, то есть установившегося течения вязкой несжимаемойжидкости в тонкой цилиндрической трубке. Закон установлен эмпирически в 1839 году Г. Хагеном, а в 1840—1841 годы — независимо Ж. Л. Пуазёйлем. Теоретически объяснён Дж. Г. Стоксом в 1845 году.
При установившемся ламинарном движении вязкой несжимаемой жидкости сквозь цилиндрическую трубу круглого сечения секундный объёмный расход прямо пропорционален перепаду давления на единицу длины трубы и четвертой степени радиуса и обратно пропорционален коэффициенту вязкости жидкости.
где
· 
— перепад давления на концах капилляра, Па;
· 
— секундный объёмный расход жидкости, м³/с;
· 
— радиус капилляра, м;
· 
— диаметр капилляра, м;
·n — коэффициент динамической вязкости, Па·с;
· 
— длина капилляра, м.
24 Гравитационное взаимодействие между телами осуществляется с помощью поля тяготения, или гравитационного поля. Это поле порождается телами и является формой существования материи. Основное свойство поля тяготения заключается в том, что на всякое тело массой m, внесенное в это поле, действует сила тяготения, т. е.
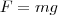(1)
Вектор g не зависит от m и называется напряженностью поля тяготения. Напряженность поля тяготения определяется силой, которая действует со стороны поля на материальную точку единичной массы, и совпадает по направлению с действующей силой. Напряженность есть силовая характеристика поля тяготения.
Сила, с которой два тела притягиваются друг к другу, называется гравитационной силой (силой тяготения). Величина этой силы определяется законом всемирного тяготения, сформулированным Ньютоном.
Не следует смешивать взаимное притяжение масс с силами магнитного или электрического притяжения. Это силы совершенно разной природы.
Силы гравитации не могут быть отталкиванием. Кроме того, гравитационное взаимодействие нельзя ослабить или устранить с помощью какого-либо экрана.
Напряжённость гравитацио́нного по́ля — векторная величина, характеризующая гравитационное поле в данной точке и численно равная отношению силы тяготения, действующей на тело, помещённое в данную точку поля, к гравитационной массе этого тела:
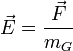
25 Космическая скорость (первая v 1, вторая v 2, третья v 3) — это минимальная скорость, при которой какое-либо тело в свободном движении с поверхности небесного тела сможет:
· v 1 (круговая скорость) — стать спутником небесного тела (то есть вращаться по круговой орбите вокруг НТ на нулевой или пренебрежимо малой высоте относительно поверхности) = 7,9 км/с
· v 2 (параболическая скорость, скорость убегания) — преодолеть гравитационное притяжение небесного тела и уйти на бесконечность = 11,2
· v 3 — покинуть звёздную систему, преодолев притяжение звезды = 46,9 км/с
26 Преобразования Галилея. Рассмотрим две системы отсчета движущиеся друг относительно друга и с постоянной скоростью v0.Одну из этих систем обозначим буквой K. Будем считать неподвижной. Тогда вторая система K¢ будет двигаться прямолинейно и равномерно. Выберем координатные оси x,y,z системы K и x',y',z' системы K' так что оси x и x' совпадали, а оси y и y', z и z', были параллельны друг другу. Найдем связь между координатами x,y,z некоторой точки P в системе K и координатами x',y',z' той же точки в системе K'. Если начать отсчёт времени с того момента, когда начало координат системы, совпадали, то x=x'+v0, кроме того, очевидно, что y=y', z=z'. Добавим к этим соотношениям принятое в классической механике предположение, что время в обеих системах течёт одинаковым образом, то есть t=t'. Получим совокупность четырёх уравнений: x=x'+v0t;y=y';z=z';t=t', названных преобразованиями Галилея. Механический принцип относительности. Положение о том, что все механические явления в различных инерциальных системах отсчёта протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится ли система или движется равномерно и прямолинейно носит названия принцип относительности Галилея. Нарушение классического закона сложения скоростей. Исходя из общего принципа относительности (никаким физическим опытом нельзя отличить одну инерциальною систему от другой), сформулированным Альбертом Эйнштейном, Лоуренс изменил преобразования Галилиея и получил: x'=(x-vt)/Ö (1-v2/c2);y'=y; z'=z; t'=(t-vx/c2)/Ö (1-v2/c2). Эти преобразования называются преобразованиями Лоуренса.
·
27 Преобразованиями Лоренца, называются преобразования, которым подвергаются пространственно-временные координаты 
каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой. Аналогично, преобразованиям Лоренца при таком переходе подвергаются координаты любого 4-вектора.
Чтобы явно различить преобразования Лоренца со сдвигами начала отсчёта и без сдвигов, когда это необходимо, говорят о неоднородных и однородных преобразованиях Лоренца.
Преобразования Лоренца без сдвигов начала отсчёта образуют группу Лоренца, со сдвигами — группу Пуанкаре, иначе называемую неоднородной группой Лоренца.
С математической точки зрения преобразования Лоренца — это преобразования, сохраняющие неизменной метрику Минковского, то есть, в частности, последняя сохраняет при них простейший вид при переходе от одной инерциальной системы отсчёта к другой (другими словами преобразования Лоренца — это аналог для метрики Минковского ортогональных преобразований, осуществляющих переход от одного ортонормированного базиса к другому, то есть аналог поворота координатных осей для пространства-времени). В математике или теоретической физике преобразования Лоренца могут относиться к любой размерности пространства.
Именно преобразования Лоренца, смешивающие — в отличие от преобразований Галилея — пространственные координаты и время, исторически стали основой для формирования концепции единого пространства-времени.
28 ри скоростях близких к скорости света масса тела увеличивается, становясь бесконечно большой при v = c:
- зависимость массы от скорости.
В теории относительности импульс определяется по формуле
Величину
называют релятивистской массой, измеренной и ИСО, относительно которой движется тело со скоростью υ.
Следовательно, 
.
При υ=c получим, что m0=m.0. Это уравнение имеет единственное решение:m0=0. Т.е. со скоростью, равной скорости света может двигаться только тело, имеющее массу покоя, равную нулю. Это говорит о предельном характере скорости света для материальных тел.
Масса движущихся релятивистских частиц зависит от их скорости:
где m 0 — масса покоя частицы, т. е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое; с — скорость света в вакууме; т — масса частицы в системе отсчета, относительно которой она движется со скоростью v. Следовательно, масса одной и той же частицы различна в разных инерциальных системах отсчета.
Один из наиболее важных законов, согласно которому физическая величина — энергия сохраняется в изолированной системе. Этому закону подчиняются все без исключения известные процессы в природе. В изолированной системе энергия может только превращаться из одной формы в другую, но ее количество остается постоянным.
29 Температу́ра (от лат. temperatura — надлежащее смешение, нормальное состояние) — скалярная физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. Температура всех частей системы, находящейся в равновесии, одинакова. Если система не находится в равновесии, то между её частями, имеющими различную температуру, происходит теплопередача(переход энергии от более нагретых частей системы к менее нагретым), приводящая к выравниванию температур в системе
Идеальный газ — математическая модель газа, в которой предполагается, что: 1) потенциальной энергией взаимодействия молекулможно пренебречь по сравнению с их кинетической энергией; 2) суммарный объем молекул газа пренебрежимо мал. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями. В расширенной модели идеального газа частицы, из которого он состоит, имеют также форму в виде упругих сфер или эллипсоидов, что позволяет учитывать энергию не только поступательного, но и вращательно-колебательного движения, а также не только центральные, но и нецентральные столкновения частиц и др
30 Закон Бо́йля — Марио́тта — один из основных газовых законов, открытый в 1662 году Робертом Бойлем и независимо переоткрытый Эдмом Мариоттом в 1676 году. Описывает поведение газа в изотермическом процессе. Закон является следствием уравнения Клапейрона[1].
Закон Бойля — Мариотта гласит:
При постоянной температуре и массе идеального газа произведение его давления и объёма постоянно.
В математической форме это утверждение записывается следующим образом
где 
— давление газа; 
— объём газа.
Важно уточнить, что в данном законе газ рассматривается, как идеальный. На самом деле, все газы в той или иной мере отличаются от идеального. Чем выше молярная масса газа, тем больше это отличие.
Закон Бойля — Мариотта, закон Шарля и закон Гей-Люссака, дополненные законом Авогадро, образуют уравнение состояния идеального газа.
31 В равных объёмах различных газов, взятых при одинаковых температуре и давлении, содержится одно и то же число молекул.
Первое следствие из закона Авогадро: один моль любого газа при одинаковых условиях занимает одинаковый объём (при н.у. этот объем равен 22.4 л)
32 Изобарический закон, открытый Гей-Люссаком в 1802 году утверждает, что при постоянном давлении объём постоянной массы газа пропорционален абсолютной температуре. Математически закон выражается следующим образом:
или
где — объём газа, 
— температура.
Если известно состояние газа при неизменном давлении и двух разных температурах, закон может быть записан в следующей форме:
или
.
Дата добавления: 2015-01-30; просмотров: 112 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Транквилизаторы. | | | Ий вопрос |