Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Уравнение Бернулли

Вторым основным законом гидродинамики является уравнение Бер­нулли, устанавливающее зависимость между скоростью и давлением в различных сечениях одной и той же струи (потока), причем эти сечения находятся на разной высоте относительно плоскости сравнения:

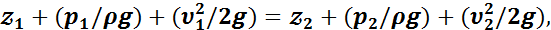(3)

где 𝓏₁ и 𝓏₂ — высоты первого и второго сечений соответственно,

р ₁ и р ₂ — давления жидкости первого и второго сечений,

υ₁ и υ₂ — скорости потока первого и второго сечений.

В общем виде уравнение Бернулли может быть представлено как

(4)

Сумма двух слагаемых, входящих в это уравнение, называется полным напором в данном сечении.

Если уравнение (4) умножить на массу F жидкости, то получим

где первые два члена представляют собой потенциальную энергию массы движущейся жидкости, а третий член — кинетическую энергию.

Таким образом, уравнение Бернулли можно сформулировать следующим образом : полный напор или сумма потенциальной и кинетической энергии движущейся жидкости есть величина постоянная для всех сечений.

Но в отличие от идеальной жидкости при движении реальной возникают потери энергии (или напора). Причины этих потерь: трение о стенки трубопровода или канала, преодоление сил внутреннего трения в вязкой жидкости. Поэтому для потока реальной жидкости напор в первом сечении

всегда будет больше, чем напор в сечении, находящемся от него на некотором расстоянии:

Если величину указанных потерь энергии обозначить h _п, то уравнение Бернулли будет иметь вид:

или

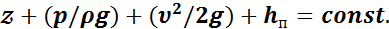
Различают два основных вида потерь:

• потери напора по длине трубопровода h _дл, обусловленные действием сил трения по поверхности канала на всех участках перемещения;

• потери местные h _м, обусловленные сопротивлением при про­хождении жидкости через изгибы, резкие сужения, расширения, отводы (тройники), краны, фильтры и т. п.

Таким образом

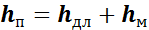
или

где ξ — коэффициент местного сопротивления определяется опыт­ным путем, для малых отверстий ξ = 0,06.