Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Геометрический смысл частных производных функции

Выясним геометрический смысл частной РїСЂРѕРёР·РІРѕРґРЅРѕР№ функции РґРІСѓС… переменных Как известно, графиком функции является некоторая поверхность. Рассмотрим точку в плоскости и соответствующую точку на поверхности. Сделаем параллельный перенос осей СЃ новым началом РІ точке и рассмотрим плоскую кривую которая получится РїСЂРё сечении поверхности РЅРѕРІРѕР№ координатной плоскостью (С‚. Рµ. плоскостью в старой системе координат). Эту РєСЂРёРІСѓСЋ можно рассматривать как гграфик функции РѕРґРЅРѕР№ переменной в плоскости (С‚. Рµ. РІ плоскости в старой системе). РќРѕ тогда, согласно геометрическому смыслу РїСЂРѕРёР·РІРѕРґРЅРѕР№ функции РѕРґРЅРѕР№ переменной, где - СѓРіРѕР» СЃ осью или, что то же, СЃ РѕСЃСЊСЋ касательной, проведенной Рє РєСЂРёРІРѕР№В РІ точке другой стороны,

Отсюда следует, что. Итак, значение частной произеодной в точке равно тангенсу угла у составленного с осью касательной, проведенной в точке к линии пересечения поверхности и плоскости у В этом заключается геометрический смысл частной производной Аналогично выясняется геометрический смысл частной производной

Дифференцируемость функции нескольких переменных

Функция Впеременных Вявляется дифференцируемой РІ точке Всвоей области определения 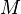, если для любой точки Всуществуют такие константы , что

РіРґРµ .

В этой записи функция

является дифференциалом функции ВРІ точке , Р° числа Вявляются частными производными функции ВРІ точке , то есть

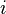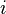РіРґРµ В— вектор, РІСЃРµ компоненты которого, РєСЂРѕРјРµ -РѕР№, равны нулю, Р° -ая компонента равна 1.

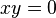Каждая дифференцируемая РІ точке функция имеет РІ этой точке РІСЃРµ частные производные, РЅРѕ РЅРµ каждая функция, имеющая РІСЃРµ частные производные, является дифференцируемой. Более того, существование частных производных РІ некоторой точке РЅРµ гарантирует даже непрерывность функции РІ этой точке. Р’ качестве такого примера можно рассмотреть функцию РґРІСѓС… переменных , равную ВРїСЂРё ВРё ВРїСЂРё . Р’ начале координат РѕР±Рµ частные производные существуют (равны нулю), РЅРѕ функция РЅРµ является непрерывной.

Это обстоятельство могло бы стать серьезной помехой всему дифференциальному исчислению функций многих переменных, если бы не выяснилось, что непрерывности частных производных в точке достаточно для дифференцируемости функции в этой точке.^[1]

необходимое условие дифференцируемости. Если функция нескольких переменных f: Rn → R дифференцируема в точке x, то у этой функции в точке x существуют все (конечные) частные производные f 0 xi(x), i = 1, n, причем коэффициенты ai в представлении равны значениям соответствующих частных производных в точке x: ai = f0 xi (x), i = 1, n. J Для дифференцируемой в точке x функции f представление (9.2) верно для любого приращения ∆x. В частности, это представление верно, если приращение ∆x имеет вид ∆x = (0... 0 ∆xi 0... 0)т, ∆xi 6= 0, где номер i выбран произвольным образом и зафиксирован. В этом случае |∆x| = |∆xi|, соответствующее полное приращение ∆f(x) функции f(x) сводится к ее i-му частному приращению

∆if(x), а равенство принимает вид

∆f(x) = ∆if(x) = ai∆xi + α(∆x)|∆xi|.

Разделив последнее равенство РЅР° ∆xi Рё перейдя Рє пределу РїСЂРё ∆xi в†’ 0, получим lim ∆xiв†’0 ∆if(x) ∆xi= ai + lim ∆xiв†’0 О±(∆x) |∆xi| ∆xi= ai,

поскольку функция α(∆x) бесконечно малая при ∆xi → 0, а отношение

|∆xi| ∆xi= ±1 ограничено, так что последний предел равен нулю. Следовательно, производная f0xi (x) в точке x существует и равна ai.