
Займемся выяснением достаточных условий дифференцируемости функции переменных. Докажем следующую теорему.
Теорема 12.10. Если функция имеет частные производные по всем аргументам в некоторой окрестности.
точки причем все эти частные производные непрерывны в самой точке то указанная функция дифференцируема в точке
Доказательство. Для сокращения записи проведем доказательство для функции РґРІСѓС… переменных Ртак, пусть частные производные существуют РІ окрестности точки и непрерывны РІ этой точке. Дадим аргументам С… Рё Сѓ столь малые приращения чтобы точка не выходила Р·Р° пределы указанной окрестности точки. Полное приращение можно записать РІ РІРёРґРµ

Выражение можно рассматривать как приращение функции одной переменной х на сегменте Поскольку функция имеет частные производные, указанная функция дифференцируема и еепроизводная по х представляет собой частную производную Применяя к указанному приращению формулу Лагранжа, найдем такое из интервала что

Рассуждая совершенно аналогично, получим

Так как производные непрерывны в точке то

где — бесконечно малые при функции. Отсюда, учитывая приведенные выражения для

и выражение для найдем

Следовательно, функция дифференцируема в точке
Для функции переменных рассуждения аналогичны, нужно только полное приращение такой функции представить в виде

Теорема доказана.
 Дифференциал ФНП.
В
ВВ Пусть функция u = F (x) определена РІ области D Рё  Вв€’ фиксированная точка. Дадим приращение каждому аргументу С… ЕЈ:
Вв€’ фиксированная точка. Дадим приращение каждому аргументу С… ЕЈ:  ВВеличину
ВВеличину  Вбудем называть вектором приращения. Р’ СЃРІРѕСЋ очередь функция u  получит приращение равное
Вбудем называть вектором приращения. Р’ СЃРІРѕСЋ очередь функция u  получит приращение равное

Определение 1. ФункцияВВ u = F (x) называется дифференцируемой РІ С‚. С…, если ее приращение может быть представлено РІ следующем РІРёРґРµ:В
ВВВВВВВВВВВВВ  ВРіРґРµ
ВРіРґРµ
A ЕЈ = A ЕЈ(x) Рё РЅРµ зависит РѕС‚ О” С…, Р° 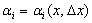 Вв€’ бесконечно малая РїСЂРё
Вв€’ бесконечно малая РїСЂРё 

Величина вектора Δ х  равна: 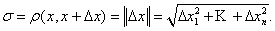
Рспользуя это обозначение, можно написать 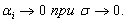
Легко показать, что 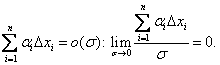
{  }
}
Определение 2. Главная и линейная часть приращения дифференцируемой функции называется дифференциалом: 
Теорема 1. Функция, дифференцируемая в т . х o − непрерывна в этой точке. { 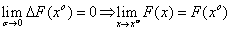 }
}
Теорема 2. (Необходимое условие дифференцируемости) Если F (x) дифференцируема в т. х, то она имеет все частные производные в этой точке, причем 
{Пусть 
 }
}
Отсюда,  ВЕсли х в€’ независимая переменная, то
ВЕсли х в€’ независимая переменная, то  Рё окончательно
и окончательно
ВВВВВВВВВВВВВВВВВВВВВВВВВВВВВВВВВ 
Теорема 3.В (Достаточное условие дифференцируемости) Пусть F(x) имеет РІСЃРµ частные производные РІ окрестности С‚.В С… РѕВ, непрерывные РІ самой этой точке. РўРѕРіРґР° функция дифференцируема РІ С‚.В С… Рѕ.
{без доказательства}
Замечание. Для дифференцируемости функции одной переменной достаточно существования производной.
В Дифференциал функции u  называют полным дифференциалом.
Определение 3. Выражение 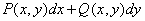 ВВназывается дифференциальной формой.
ВВназывается дифференциальной формой.
Теорема 4. Дифференциальная форма является полным дифференциалом некоторой функции u (х, у) тогда и только тогда, когда выполнено условие 
{1.Необх.:  Тогда
РўРѕРіРґР° 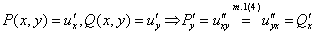
2. Дост. – без доказательства}
Пример. Найти общее решение дифференциального уравнения:ВВВВВ
ВВВВВВВВВВВВВВ 
В
В§6. Геометрический смысл дифференцируемости. Касательная плоскость Рё нормаль РєВВВВВВВВВВВ
В ВВВ поверхности.
ВВВ Рассмотрим поверхность S: z = f (x,y), дифференцируемую РІ С‚.  S.
S.
Определение 1. Плоскость, проходящая через т. М 0, называется касательной плоскостью к поверхности S в т. М 0, если угол между ней и секущей (М 0 М 1) ( ) стремится к нулю при
) стремится к нулю при  .
.
Определение 2. Вектор, ортогональный к касательной плоскости в т. М 0, называется нормальным вектором к поверхности в этой точке. Нормалью к поверхности называется
прямая, проходящая через т. М 0 перпендикулярно касательной плоскости в этой точке.
 Обозначим  ,
,  . Вектор приращения:
. Вектор приращения:  В
В
В РР· условия дифференцируемости функции z  следует, что 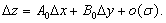
В Рассмотрим плоскость  ВРё СѓРіРѕР» П† между секущей Рё этой плоскостью:
ВРё СѓРіРѕР» П† между секущей Рё этой плоскостью:  ВРїСЂРё
ВРїСЂРё  Отсюда сразу следует, что плоскость Рџ – касательная Рє поверхности РІ С‚. Рњ 0. Р’ результате имеем:В
Отсюда сразу следует, что плоскость Рџ – касательная Рє поверхности РІ С‚. Рњ 0. Р’ результате имеем:В
Функция z = f (x,y), дифференцируемая РІ некоторой точке (С… 0, Сѓ 0) имеет РІ соответствующей С‚. Рњ 0 касательную плоскость: 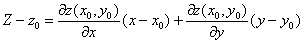 ВРё нормальный вектор
ВРё нормальный вектор 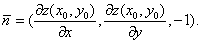
Дата добавления: 2015-02-16; просмотров: 104 | Поможем написать вашу работу | Нарушение авторских прав |