Читайте также:
|
Инвариантность законов механики в отношении преобразований Галилея
(принцип относительности Галилея – механический принцип относительности);
2) инвариантность времени – независимость хода времени для наблюдателей в различных инерциальных системах отсчета (
). Это иначе можно сформулировать как абсолютность времени.
Напомним также, что преобразования Галилея – это правила перехода от описания процесса в одной инерциальной системе отсчета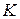 
к описанию того же процесса в другой системе 
.
Следствием из этих постулатов и преобразований Галилея являются, в частности, классическое правило сложения скоростей, а также представление об инвариантности пространственного интервала: 
.
Таким образом, классическая механика тесно связана с представлениями об абсолютном времени и об абсолютном пространстве – их свойства не зависят ни от каких обстоятельств.
Установленные экспериментально факты (законы электродинамики, постоянство скорости света в вакууме) заставили переосмыслить основания механики. В частности Эйнштейном был обобщен принцип относительности, а также взамен постулата об инвариантности времени предложен постулат об инвариантности скорости света). Новые постулаты привели к новым правилам перехода между инерциальными системами отсчета (преобразованиям Лоренца), а также и другим важным следствиям.
Следствия из постулатов и преобразований координат и времени
Принцип неизменности хода времени и неизменности скорости света исключают друг друга. Это разные по смыслу и происхождению постулаты двух теорий – классической механики и специальной теории относительности (СТО). Характер постулатов радикально влияет на выводы основанных на них теорий. Убедимся в этом, сопоставив основные выводы из постулатов ньютоновской механики и СТО.
| Будем производить такое сопоставление на основе описания движения тела А, показанного на рисунке. Для описания будем применять две инерциальные системы отсчета: К и К '. Они отличаются только движением системы К ' относительно К со скоростью v, направленной только вдоль одной из осей координат (х). Для простоты считаем, что вдоль двух других осей движение не происходит. | 
| ||
| Будем считать также, что тело А движется относительно системы К ' вдоль оси х ' со скоростью u ', а относительно К – со скоростью u. | |||
| Две теории сопоставим с помощью таблицы, сравнивая их в каждой строке постулаты и выводы теорий. | |||
| Примечания: СТО можно применять не только к механическим процессам, она имеет и другие области применения. Применение же СТО для моделирования механического движения приводит к частному случаю этой теории, который называют релятивистской механикой. Именно она и представлена в левой части таблицы. В правой части таблицы отражены положения классической ньютоновской механики. Для полноты картины в таблице сопоставлены также и постулаты двух теорий, и правила преобразования координат. | |||
| Классическая механика (МЕХАНИКА Ньютона) | сПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (Релятивистская механика) | ||
| Исходные положения (постулаты) теорий | |||
| 1. Принцип относительности Галилея (механический принцип относительности): В любых инерциальных системах отсчета все механические явления протекают (и описываются) одинаково. | 1. Принцип относительности Эйнштейна (обобщенный принцип относительности): В любых инерциальных системах отсчета все физические явления протекают (и описываются) одинаково. | ||
2. Принцип инвариантности времени:
В любых инерциальных системах отсчета ход времени одинаков: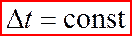 
| 2. Принцип инвариантности скорости света:
В любых инерциальных системах отсчета скорость света в вакууме одинакова: 
| ||
| Правила преобразования координат и времени, удовлетворяющие постулатам | |||
Преобразования Галилея:
| Преобразования Лоренца:
 
| ||
При малых скоростях движения (v << c) преобразования Лоренца совпадают с преобразованиями Галилея. В этом проявляется действие принципа соответствия физических теорий.
Продолжение таблицы
| Классическая механика (МЕХАНИКА Ньютона) | сПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (Релятивистская механика) | |
| Следствия из постулатов обеих теорий и правил преобразования координат и времени | ||
1. Правило сложения скоростей
(классическое):
| 1. Правило «сложения» скоростей
(релятивистское):
| |
2. Формула для временного интервала
между событиями 1 и 2:
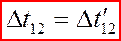Интервал времени  , отсчитываемый по часам, движущимся вместе с объектом со скоростью v (собственное время в подвижной системе) такое же, как и по часам в неподвижной системе отсчета  , т.е. время абсолютно.
| 2. Формула для временного интервала
между событиями 1 и 2:
Время в неподвижной системе отсчета длиннее собственного времени в подвижной системе (эффект релятивистского замедления времени при движении). Т.е. время относительно. Нет единого мирового времени. В каждой системе отсчета оно свое.
| |
Продолжение таблицы
| Классическая механика (МЕХАНИКА Ньютона) | сПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (Релятивистская механика) | |
3. Формула для пространственного интервала
между точками 1 и 2:
| 3. Формула для пространственного интервала
между точками 1 и 2:
| |
| Длина тела (пространственный интервал) не зависит от скорости относительного движения систем отсчета, в которых описывают движение этого тела. Т.е. пространство абсолютно. | Пространственный интервал  – длина тела в системе отсчета, относительно которой оно движется, меньше, чем длина  в системе, где тело покоится. (Эффект релятивистского сокращения длины).
Т.е. пространство относительно.
| |
Итак, пространственный интервал и временной интервал с точки зрения СТО относительны. Это свидетельствует об относительности пространства и относительности времени. (Заметим, что название этой теории и отражает возникшее после ее появления представления об относительности пространства и времени: теория относительности пространства и времени).
В отношении новых представлений о пространстве и времени СТО этим выводом не ограничивается. В СТО найдена пространственно-временная характеристика, которая не меняется при переводе описания природных процессов из одной инерциальной системы в другую. Это так называемый пространственно-временной интервал.
Дата добавления: 2015-02-16; просмотров: 69 | Поможем написать вашу работу | Нарушение авторских прав |